Magic Matrix
Find out why these matrices are magic. Can you work out how they were made? Can you make your own Magic Matrix?
Age
7 to 11
Challenge level
Problem
Here is a "magic" matrix:
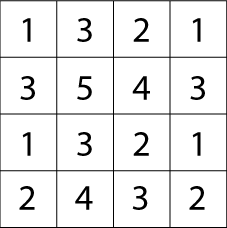
It doesn't look very magical does it?
This is how you find out the "magic" in the matrix:
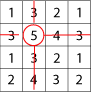
Circle any number in the matrix, for example, $5$. Draw a line through all the squares that lie in the same row and column as your selected number:
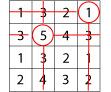
Repeat for a third time, for example:
Then circle only the remaining number that has no line through it:
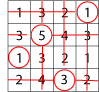
Add all the circled numbers together and note your answer.
Try again with a different starting number. What do you notice?
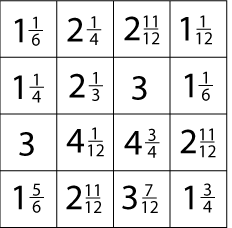
Try the same thing with these two slightly harder matrices:
This problem was made to celebrate NRICH's tenth birthday - perhaps you can see the connection!
Let's try a different one with larger numbers.
Now make an addition table like this:
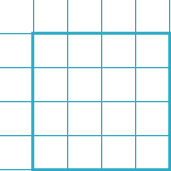
You can download a sheet of them here.
Put your numbers in the cells on the outside and add them to make the matrix:
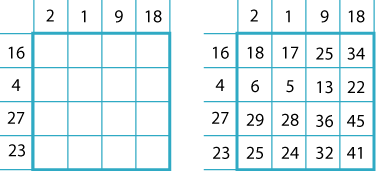
Finally, copy the square without the numbered outside cells:
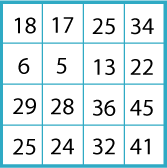
Now you know how the matrix works, you are ready for the real problem.
Can you work out what numbers were used to make any of the original three matrices?
Image
It doesn't look very magical does it?
This is how you find out the "magic" in the matrix:
Circle any number in the matrix, for example, $5$. Draw a line through all the squares that lie in the same row and column as your selected number:
Image
Then circle another number that has not got a line through it, for example, the $1$ in the top right hand corner, and again cross out all squares in the same row and column:
Image
Repeat for a third time, for example:
Image
Then circle only the remaining number that has no line through it:
Image
Add all the circled numbers together and note your answer.
Try again with a different starting number. What do you notice?
Try the same thing with these two slightly harder matrices:
Image
|
Image
|
This problem was made to celebrate NRICH's tenth birthday - perhaps you can see the connection!
Let's try a different one with larger numbers.
Image
What is the magic total this time?
I will show you how this kind of matrix works. You can then invent one to try on your friends!
First you need to choose your 'magic total'. As you know, I chose $100$ for the matrix above.
I have chosen: $1, 16, 9, 23, 18, 4, 2$ and $27$. [You can check that together they add to $100$.]
Now make an addition table like this:
Image
You can download a sheet of them here.
Put your numbers in the cells on the outside and add them to make the matrix:
Image
Finally, copy the square without the numbered outside cells:
Image
Now you know how the matrix works, you are ready for the real problem.
Can you work out what numbers were used to make any of the original three matrices?
Getting Started
You could start with the numbers in the top row of the matrix. What two numbers could be added together to make $1$?
Why not write them in, one to the left of the row and one above the number $1$ in the matrix. Now, you could fill in the rest of the numbers which will add to make that top row. Test out your numbers by looking at the second row.
Be prepared to start again if it doesn't work!
Student Solutions
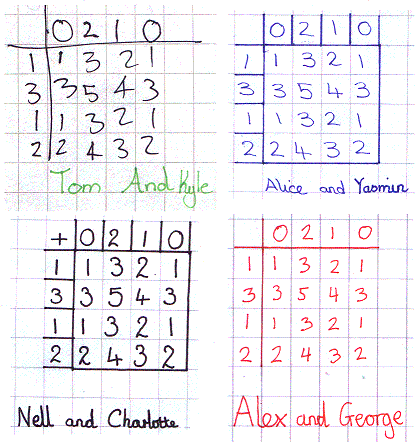
Several of you noticed that the numbers you end up with in the matrix always add up to 10 - to fit in with NRICH's 10th anniversary! A whole group of pupils from Gorseland Primary School worked hard on the first matrix in pairs, discovering how it works, making their own and solving this problem. They found this solution for the first matrix:
Image
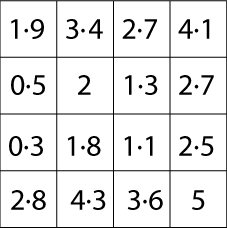
George from Greenwich solved the second and third matrices as well. For the second one, he says:
The numbers on the sides are the eight magic numbers, they are 1.7, 0.3, 0.1, 2.6, 0.2, 1.7, 1 and 2.4. The eight numbers add up to 10 and they fit in place:| 0.2 | 1.7 | 1 | 2.4 | |
| 1.7 | 1.9 | 3.4 | 2.7 | 4.1 |
| 0.3 | 0.5 | 2 | 1.3 | 2.7 |
| 0.1 | 0.3 | 1.8 | 1.1 | 2.5 |
| 2.6 | 2.8 | 4.3 | 3.6 | 5 |
For the third matrix, George says:
What you have to do in the first step is convert all the fractions to a common denominator to make it easier. The common number is 12. This is the solved grid below. As you can see, the eight numbers are 8/12, 6/12, 19/12, 27/12, 5/12, 9/12, 30/12 and 16/12. They add up to 10 as well.| 6/12 | 19/12 | 27/12 | 5/12 | |
| 8/12 | 14/12 | 27/12 | 35/12 | 13/12 |
| 9/12 | 15/12 | 28/12 | 36/12 | 14/12 |
| 30/12 | 36/12 | 49/12 | 57/12 | 35/12 |
| 16/12 | 22/12 | 35/12 | 43/12 | 21/12 |
You can check that this is the same as the matrix in the problem! Excellent George, thank you for sending in your solutions.
Teachers' Resources
Magic Matrix
Here is a "magic" matrix:Image
It doesn't look very magical does it?
This is how you find out the "magic" in the matrix:
Circle any number in the matrix, for example, $5$. Draw a line through all the squares that lie in the same row and column as your selected number:
Image
Then circle another number that has not got a line through it, for example, the $1$ in the top right hand corner, and again cross out all squares in the same row and column:
Image
Repeat for a third time, for example:
Image
Then circle only the remaining number that has no line through it:
Image
Add all the circled numbers together and note your answer.
Try again with a different starting number. What do you notice?
Try the same thing with these two slightly harder matrices:
Image
|
Image
|
This problem was made to celebrate NRICH's tenth birthday - perhaps you can see the connection!
Let's try a different one with larger numbers.
Image
What is the magic total this time?
I will show you how this kind of matrix works. You can then invent one to try on your friends!
First you need to choose your 'magic total'. As you know, I chose $100$ for the matrix above.
I have chosen: $1, 16, 9, 23, 18, 4, 2$ and $27$. [You can check that together they add to $100$.]
Now make an addition table like this:
Image
You can download a sheet of them here.
Put your numbers in the cells on the outside and add them to make the matrix:
Image
Finally, copy the square without the numbered outside cells:
Image
Now you know how the matrix works, you are ready for the real problem.
Can you work out what numbers were used to make any of the original three matrices?
Why do this problem?
This problem starts very easily but becomes harder with the second and third matrices. The last part, discovering how to work out how the matrix is made up, is really challenging because there are so few clues.Possible approach
You could start by doing the first magic matrix on the board together. It is not very surprising when all get the same answer! If anyone gets $11$, for example, instead of $10$, you can check quickly that they are doing it correctly. Then let the class try another couple for themselves, perhaps suggesting that they make sure they choose different numbers from their neighbours. Those
confident with decimals and fractions could try then the next two matrices. This sheet gives six copies of the first matrix and three copies for each of the second and third ones.
After that you could introduce the next matrix with the magic total of $100$, and then continue to show the class how it is built up. For this purpose you can use this sheet with the illustrations from the problem.
After this, the group could be challenged to work in pairs making their own magic matrices. It is advisable to limit these to magic totals between $12$ and $200$. This sheet has six copies of the frame for the matrix. However, squared paper can easily be used
instead.
The final challenge, to discover what numbers were used to make any of the original three matrices is hard, and could, perhaps, be reserved for the most able learners.
Key questions
Why not try one of the other matrices?
How can the same number result whichever choices are made?
What number are you choosing for your own matrix?
How are you going to divide it into eight numbers?
You could start with the numbers in the top row of the matrix.
What two numbers could be added together to make $1$?