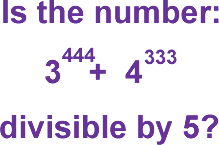Big Powers
Three people chose this as a favourite problem. It is the sort of problem that needs thinking time - but once the connection is made it gives access to many similar ideas.
Problem
Getting Started
What determines whether a number is divisible by $5$ or not?
Find: $3^{1}, 3^{2}, 3^{3}, 3^{4}, 3^{5}, 3^{6}, 3^{7}, 3^{8}, 3^{9} \ldots$
What do you notice?
Find: $4^{1}, 4^{2}, 4^{3}, 4^{4}, 4^{5}, 4^{6}, 4^{7}, 4^{8}, 4^{9} \ldots$
What do you notice?
Student Solutions
In the main, successful solvers of this problem went about it in one of two ways.
One way was to `break it down' and study the end digit for a set of powers. This is what Samantha and Zoe of Maidstone Girls' Grammar School and Angela from Hethersett High in Norfolk did.
Another way was to look at some remainders when dividing by $5$. This is what Avishek, James, Martin, Thomas, Kintel and Marcus from Simon Langton Boys' School did.
This is Angela's solution:
Teachers' Resources
At first glance, a challenging problem; but no algebra is required to justify the solution.
Students who meet this problem for the first time may need a significant amount of support in structuring a solution so it is useful to be able to find similar tasks to which they may apply their new-found understanding.
It is important to be able to justify any pattern. How can you be sure it continues?