Compare Areas
Which has the greatest area, a circle or a square, inscribed in an isosceles right angle triangle?
Problem
ABC is an isosceles right angled triangle.
Each diagram has a different shape inscribed within it.
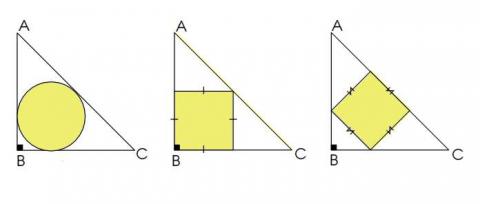
Which of the inscribed figures has the greatest area?
Click here for a poster of this problem.
Getting Started
Which lengths are equal in the diagrams?
Which angles are equal?
Let AB = BC = 12cm
Have a go at drawing each diagram.
Of the two squares, which has the greatest area?
How do you know?
Draw the radii at the points where the circle touches the triangle.
If the radius of the circle is r, can you find the hypotenuse of the triangle in terms of r?
Student Solutions
Many students got the correct answer that the circle which is embedded inside the isosceles triangle is the largest of the three shapes.
Some students measured the diagrams given which luckily had been drawn accurately to scale, while others observed the symmetry of the isosceles triangle and the consequences of joining B to the mid point of AC. To find the radius of the circle it helps to draw perpendiculars from the centre to the sides of the triangle.
Taking the lengths of the short sides of the triangle as $2$ units:
the radius of the circle is found to be $2-\sqrt{2}$ and the area to be $\pi (6 - 4\sqrt{2})$.
the side length of square one to be $1$ and area $1$;
and the side length of square two to be $\frac{2\sqrt{2}}{3}$ and area $\frac{8}{9}$.
Many students evaluated the ratio of the areas as $1.078 : 1: 0.889$ (to $3$ dec. places)
Ben and Adrian from the Simon Langton Grammar School for Boys used trig ratios, as did Hannah of Maidstone Girls Grammar School, to arrive at the same conclusions.
Teachers' Resources
Why do this problem?
This problem brings together ideas of areas of circles and squares, the use of Pythagoras' Theorem and the property of tangents to a circle from an external point.
Possible approach
You might start with the middle diagram which is the easiest. It brings in the ratio of the sides of an isosceles right angles triangle which is again used in the other two parts.
Key questions
If you know the side length of an isosceles right angled triangle how do you find the hypotenuse?
Which lengths are equal in the diagram?
Which angles are equal?
Can you use the symmetry of the diagram?
