You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Triangle Incircle Iteration
Keep constructing triangles in the incircle of the previous triangle. What happens?
Medallions
Three circular medallions fit in a rectangular box. Can you find the radius of the largest one?
Age 14 to 16
Challenge Level
ABC is an isosceles right angled triangle.
Each diagram has a different shape inscribed within it.
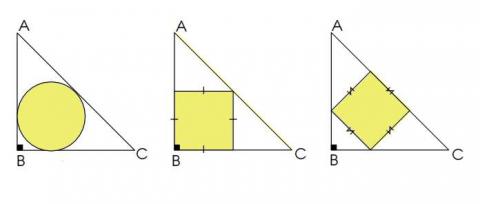
Which of the inscribed figures has the greatest area?
Click here for a poster of this problem.
Copyright © 1997 - 2023. University of Cambridge.
All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.
NRICH is part of the family of activities in the Millennium Mathematics Project.