Twin corresponding Sudoku
This sudoku requires you to have "double vision" - two Sudoku's for the price of one
Problem
By Henry Kwok
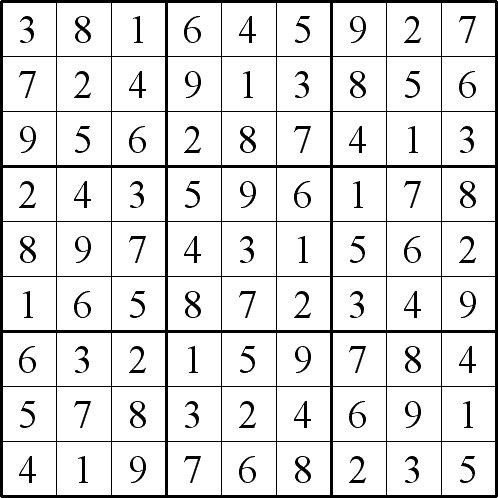
Twin A
Image
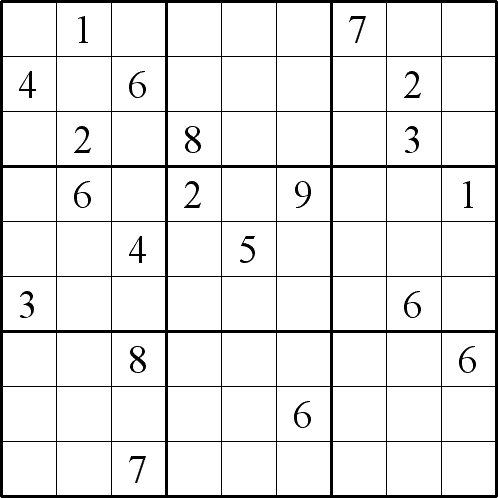
Twin B
Image
Rules of Twin Corresponding Sudoku
As with all the Sudoku puzzles published here, the object is to fill in the whole of each 9x9 grid with numbers 1 through 9 (one number per cell) so that each horizontal line, each vertical line, and each of the nine 3x3 squares (outlined with the bold lines) contain all the nine different numbers 1 through 9.
This problem is different because it consists of a pair of linked standard Sudoku puzzles each with some starting digits. To get a complete solution for the twin puzzles, we have to solve each twin puzzle with the usual strategies but we can only get the complete solution for the twin puzzles by substituting the equivalent values of the digits from one twin Sudoku into the other. So, for example, we can see that in (2,1), that is row 2 column 1, twin A contains the number 4 and twin B contains the number 7. This means that everywhere a 4 appears in twin A - a 7 appears in twin B and vice versa. This immediately gives you some more starting digits in each twin!
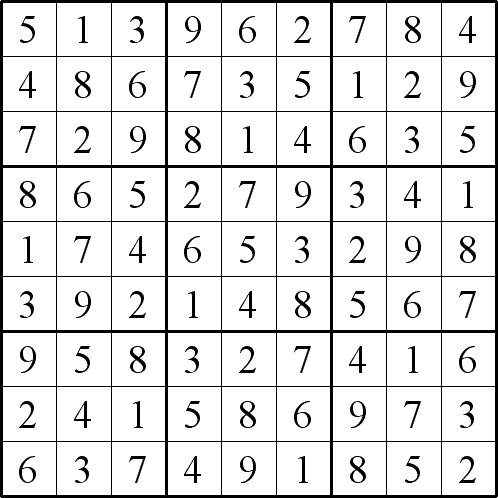
Student Solutions
Twin A
Image
Twin B
Image