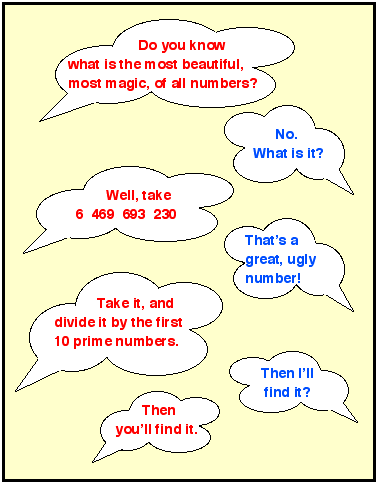
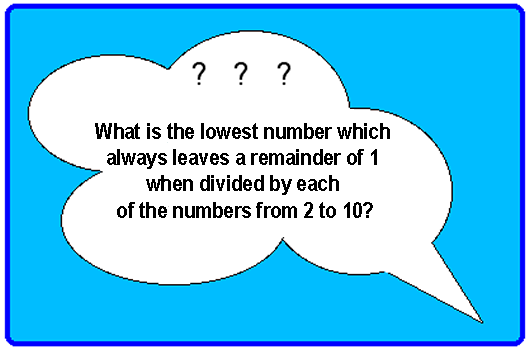Difficulties with Division

A lot of teachers struggle with teaching division to children and I have been thinking about this recently. I think there are a number of factors contributing to this. Firstly, by the middle of Stage 2 there is a huge range of level of understanding of the concept of division and secondly the concept itself can be thought of as building on children's understandings of addition, subtraction and multiplication. The spread of different levels of understanding is likely to make any class "mixed ability" for this topic. There are also difficulties with the written algorithm. Altogether, it is a complicated picture.

Let us try to unravel this a little and find some interesting problems that might help us to help our pupils. We'll start with the different conceptions of division that are commonly used in schools. We basically have three different ideas that we use with children and we often switch between the languages of each without thinking about the confusions this might cause for the children.

Division is often introduced as "sharing" and this is certainly one of the simplest approaches. We look at problems that involve sharing a number of items between a number of different people. We don't necessarily need to know how many items are in our original pile or how many people we are sharing them between to be talking about division in this way, and so this conception doesn't easily lead to the representation of the situation in the form of a mathematical expression such as $12\div 4=3$. At this stage children need lots of experience with sharing physical objects out and expressing what they are doing in words and then in symbols. An interesting problem that works with this idea is Lots of lollies .

 

Image

A second conception of division is that of grouping and this links to ideas about successive subtraction. In this setting the problem is about how many groups of a given number you can make out of a pile of items - "How many groups of $3$ there are in $12$?" for instance. This links with ideas of division as inverse multiplication and children can be offered plenty of opportunities to explore patterns in the multiplication tables and to express them in all the different ways that are possible, in words and in symbols. For instance, our example of $3\times 4=12$ generates a whole lot of sentences and symbolic expressions:

Three lots of four make twelve

$4\times 3=12$

Four lots of three make twelve

There are three groups of four in twelve

$12\div 4=3$

There are four groups of three in twelve

$12\div 3=4$

If you share twelve things between three people they will have four things each

$12\div 3=4$

If you share twelve things between four people they will have three things each

$12\div 4=3$

It is important that children grasp the equivalence of all these different expressions in order to develop their facility with division. In their delightful book Williams and Shuard outline three stages in understanding division as:

 

1. Using grouping and sharing as different operations and solving problems using concrete apparatus
2. Relating sharing to grouping
3. Using their knowledge of multiplication to deal with both types of division by the same numerical procedure

These should be accomplished by working through the activities like the one above and encouraging children to communicate with one another about their understanding.

Working on from using known facts, the next problem arises with the written algorithms for division. Unlike the other standard algorithms for addition, subtraction and multiplication, the standard algorithm for division is worked from left to right and the setting down seems totally different. Despite much advice about not introducing written algorithms too early, many children meet it before they are ready to understand it and without being given enough chance to develop their own strategies for dividing large numbers. Stuart Plunkett's comment made way back in 1978 still rings true:

"Children should be helped to acquire sensible methods for calculating''

The value of informal jottings to record division calculations has been outlined by Julia Anghileri and she shows some interesting analysis in the book "Teaching Number Sense''. Before children embark on any formal recordings using the standard algorithm for division they need plenty of familiarity with tables and number patterns in them as well as practice with mental strategies such as chunking, doubling and halving.

All of these activities do require a lot of practice and experience but once you are confident that your class have had a good grounding in these areas, why not try some of these problems?

Image

Image