Multiples Grid
What do the numbers shaded in blue on this hundred square have in common? What do you notice about the pink numbers? How about the shaded numbers in the other squares?
Problem
Multiples Grid printable sheet
Here is a 100 grid with some numbers shaded:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
For accessibility, clicking on the 'show' button below a table in this activity will show a description of the table.
Pink numbers: 5, 10, 15, 20, 25, 30, 40, 45, 50, 55, 60, 65, 75, 80, 85, 90, 95, 100
Blue numbers: 7, 14, 21, 28, 42, 49, 56, 63, 77, 84, 91, 98
Purple numbers: 35, 70
Orange numbers: all others
What do all the numbers shaded blue have in common?
What do you notice about all the numbers shaded pink?
Can you work out why two of the numbers are shaded in a purple colour?
Now, here is part of a 100 square shaded in a different way:
| 24 | 25 | 26 |
| 34 | 35 | 36 |
| 44 | 45 | 46 |
Pink numbers: 24, 26, 34, 36, 44, 46
Blue number: 35
Orange numbers: 25, 45
Can you explain the shading this time?
Here are some more parts of the 100 square, each one shaded according to different rules. Can you work out what the rules are for each?
Is there only one solution each time?
| 66 | 67 | 68 |
| 76 | 77 | 78 |
| 86 | 87 | 88 |
Blue numbers: 66, 77
Purple number: 88
Orange numbers: 67, 68, 76, 78, 86, 87
| 34 | 35 | 36 |
| 44 | 45 | 46 |
| 54 | 55 | 56 |
Purple numbers: 36, 54
Blue number: 45
Orange numbers: 34, 35, 44, 46, 55, 56
| 5 | 6 | 7 |
| 15 | 16 | 17 |
| 25 | 26 | 27 |
Pink number: 16
Blue number: 27
Orange numbers: 5, 6, 7, 15, 17, 25, 26
This problem is featured in Maths Trails: Excel at Problem Solving, one of the books in the Maths Trails series written by members of the NRICH Team and published by Cambridge University Press.
Getting Started
There is a clue in the title of the problem!
You may like to investigate this spreadsheet which shades the numbers on the $100$ square. The pictures have been taken from this spreadsheet. Can you see what is happening?
Are there some answers which you can rule out straight away in each case?
How will you know you have all the solutions for each grid?
Student Solutions
Lulu and Sophie from St. Nicolas C. of E. Junior School, Newbury have sent us a solution to the Multiples Grid problem. Thank you both! For the first large square, they say:
The blue numbers are all multiples of 7.
The pink numbers are all multiples of 5.
In this square:
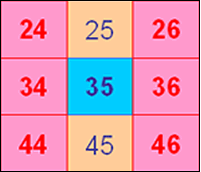
they say:
Are you sure the blue could be multiples of 5? In this square:
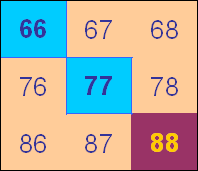
they say:
The blue numbers are multiples of 11.
The pink numbers are supposed to be multiples of 8.
In the next square:
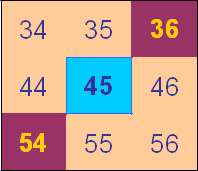
they explain:
The blues are multiples of 9.
The pinks are multiples of 6.
Finally, in this last square:
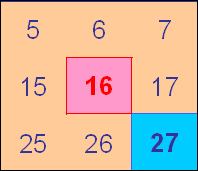
Sophie and Lulu wrote:
The blues are multiples of 9.
Thank you for sending us your solution, girls. Well done!
Teachers' Resources
Why do this problem?
This problem is an interesting way of reinforcing understanding of factors and multiples.
Possible approach
To start with, ask children to talk in pairs about why the numbers in the first 100 square are shaded blue, pink and purple. Invite them to share their ideas and encourage correct use of vocabulary.
Learners could continue to work in pairs, perhaps using the second page of the printable sheet, which shows the four parts of differently-shaded 100 squares. As they work on the problem, trying to find out which factors have been chosen in order to produce the shading, encourage them to justify their solutions to their partners, and perhaps then to the whole class. How are they going about the task? It might be useful to discuss ways of working systematically so that no solutions are omitted.
This spreadsheet, which shades the squares according to the chosen factors, can be used to check their hypotheses. In a plenary session, you could use the second sheet of the spreadsheet to pre-prepare some shaded sections of the 100 grid without numbers. If you tell them which multiples have been shaded, can the class work out where the small part of the 100 grid is, i.e. which numbers it contains?
Key questions
Possible extension
Learners could explore the spreadsheet for themselves at a computer. Challenge them to make up their own questions to ask a friend.
Possible support
A multiplication square may be useful for those children who find instant recall of multiplication facts difficult.
