Odd Differences
The diagram illustrates the formula: 1 + 3 + 5 + ... + (2n - 1) = n² Use the diagram to show that any odd number is the difference of two squares.
Problem
The diagram illustrates the formula: 1 + 3 + 5 + ... + (2n - 1) = n ² Use the diagram to show that any odd number is the difference of two squares. Note that 15 = 8 ² - 7 ² as well as 4 ² - 1 ². Write the number 105 as the difference of two squares in as many different ways as you can? The number 1155 can be written as the difference of two squares in eight different ways, can you find them? | Image
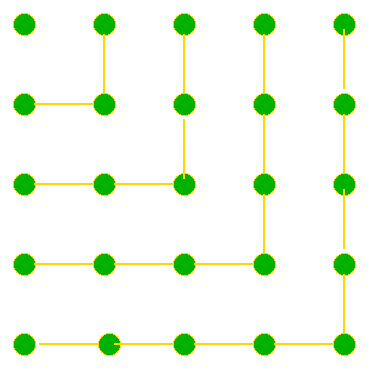
|
Student Solutions
Tom started us off with the following idea. Thanks Tom.
In the square of dots you can imagine the"L" of any odd number and if you take the square for the odd number below it from the square of the odd number you get the number you stated with. To find the two squares you have to find half the odd number and round it up and down. So half of $13$ is $6.5$ so the two squares have sides $7$ and $6$.
Here is a picture:
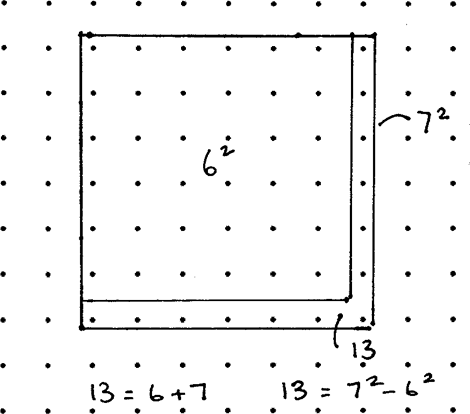
So, using the diagram you know that $$105= \frac{105-1}{2} + \frac{105+1}{2}$$
$$ 105 = 52 +53$$
$$ 105 = 53^2 - 52^2$$
You can always find one way using this method. So
$$1155= \frac{1155-1}{2} + \frac{1155+1}{2}$$
$$ 1155 = 577+578$$
$$ 105 = 578^2 - 577^2$$
Alex, from the Grammar School at Leeds extends the algebra building on the second visualisation:
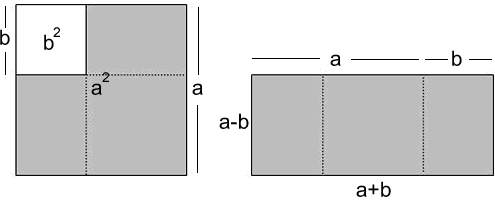
Teachers' Resources
Why do this problem :
This connection between the set of odd numbers and squares is not often encountered in school and offers a very accessible example of visualisation.
The 'difference of two squares' is a key algebraic transformation and problems like this can lead students into a deeper appreciation of that form through a further visualisation.
Possible approach :
Remind them of the identity $a^2 - b^2 = (a + b)(a -b)$ and give them time to consider and see the connection with what they have already done. For example: $$9=5^2 - 4^2 = (5+4)(5-4).$$
At this point another visualisation might be useful in order to suggest how further differences might be found.

The problem of writing the number $105$ as the difference of two squares becomes a problem about factor pairs that make a product of $105$.
Draw out from the students how this transformation helps [we now seek factors of $105$ rather than guessing squares and calculating differences].
Key questions :
- Explain how this image shows us the sum of the first n odd numbers - what is that sum ?
- For $105$ (and then for $1155$) how many ways might there be, and why do you think that ?
Possible extension :
Possible support :
