Wallpaper
These pieces of wallpaper need to be ordered from smallest to largest. Can you find a way to do it?
Problem
Arrange these pieces of wallpaper in order of size. Put the smallest first.
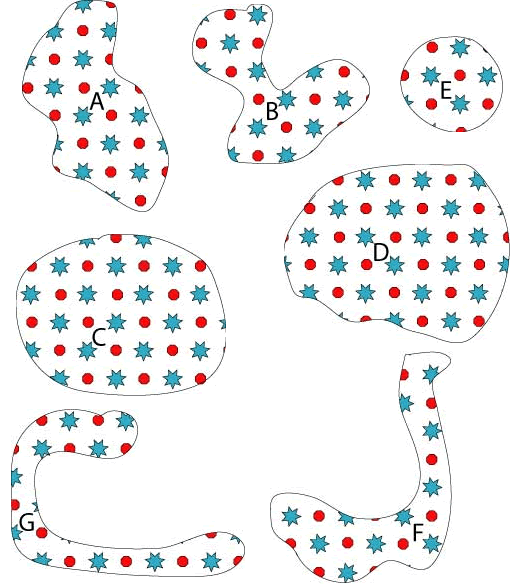
You may find it helpful to print off this sheet.
Can you explain how you did it?
Getting Started
Perhaps you will need to think or talk about what you mean by biggest and smallest first.
How might the pattern on the wallpaper help?
Student Solutions
Ayati from Chippenham Primary School wrote:
From smallest to largest, I have worked out the size order as E, G, B, F, A, C, D. I did this by counting how many complete blue stars there were in each scrap of wallpaper. It was easier and more efficient.
Jonah and Adeline from Pratt Community School in the United States sent in this excellent explanation:
First, we boxed each shape and we measured the perimeter of all of the shapes. We measured in inches. But this did not work, because the shapes are curved and it is difficult to box the shapes precisely. As a consequence, we could not find a precise perimeter. For example, it is easier to box D, E and C - because these are oval or round shapes. Shapes like G and F were difficult to find the accurate measurement. We thought about - what if we could stretch G and F out, to an easier shape to find the perimeter. But then we realized that the shapes would have the same number of dots, whether they were stretched out or not.
So, we tried something different. We thought that the stars and dots would help us find the area of each shape. First, we counted all the whole stars and whole dots. Then we realized that we could add the half shapes together to make another whole.
Based on counting the dots and stars, here is the order from smallest to biggest:
E = 10 G = 19 B & F (tied) = 20 A = 24 C = 33 D = 39
Bea, from the same school, sent in the following together with a picture:
First, I tried to imagine that I could fold the shapes so that they would be similar. For example, I imagined that I could fold the top of F down so that it would be similar to C and D.
I realized that no matter how much I stretched it, it would not give me an accurate measure of the perimeter. So, I decided to look at the stars and the dots - the inside. I drew lines from shape to shape. A line from star to dot and dot to star counted as 1 line segment. I followed that strategy with every shape.
Then I counted the line segments. Here's the order from smallest to biggest:
E = 5 G = 11 B = 13 F = 15 A = 21 C = 29 D = 32

Thank you for all the solutions. B and F are very similar in size, so we think they could go either way round in the order.
Teachers' Resources
Why do this problem?
This activity is designed to help children begin to understand the meaning of area. It is a follow-up to Sizing Them Up and it makes an explicit link to the concept of area. The context of wallpaper or wrapping paper might be familiar to some children and therefore might hook them in and capture their curiosity.
Possible approach
In this challenge, pupils can use the pattern on the wallpaper to count the number of stars and/or spots inside each piece so that they should end up with the same ordering. It is likely that they will spend some time discussing how best to approach this problem before reaching that conclusion.
If they do not suggest counting the stars and spots you could say something like, "I wonder how many stars there are on this shape?". This could lead into a discussion about why it might be useful for everyone to have the same way of working out how much space is covered by an object - perhaps relating it to a sports pitch or a tablecloth.
Key questions
How might the pattern on the wallpaper help?
Possible extension
You could extend the challenge by adding in a piece of wallpaper or wrapping paper of your own which has a different pattern and ask the children to cut different shapes of the "same size".
Possible support
Suggest counting the stars and spots on each shape and recording them in some way.
