Brush Loads
How can you arrange the 5 cubes so that you need the smallest number of Brush Loads of paint to cover them? Try with other numbers of cubes as well.
Problem
We have five cubes and we're going to join them together, following a few simple rules:
- the cubes must be together face-to-face;
- they must not topple over.
We're going to paint the faces that can be seen. One Brush Load (a kind of unit that we'll use) will paint one square face.
For example, here are five cubes joined together:
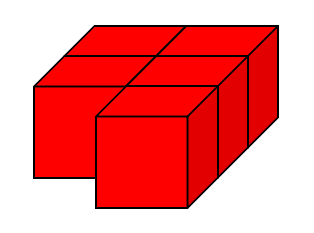
Counting the faces to be painted comes to 15, so 15 Brush Loads (or BLs) are needed. Remember we're only counting visible faces, so not those that are touching the surface where the cubes are placed.
But of course we could have placed the five cubes differently, for example:
Counting the faces to be painted now, we have 17, so 17 BLs.
Can you find ways of arranging five cubes so that:
- you need as few BLs as possible?
- you need as many BLs as possible?
Can you find arrangements that need all the numbers between the largest and the smallest numbers of BLs?
What happens if you use more cubes, for example 6, 7, 8...?
Can you find out the smallest number of BLs and the largest number of BLs possible in each case?
Can you predict the arrangements which need as few BLs as possible and as many BLs as possible?
Getting Started
You could use Multilink cubes to try out your ideas.
Remember, once the shape is made there is no picking it up to count "underneath" as these faces would not be painted!
Student Solutions
Well done to everybody who had a go at this activity.
Lots of children said that the smallest number of brush loads needed was 15 and the largest number was 21. Dana from Twyford School in the UK made arrangements of cubes that used all of the numbers of brush loads between 15 and 21, and she even found a way to make an arrangement using 22 brush loads! Have a look at Dana's solution to see how she did it.
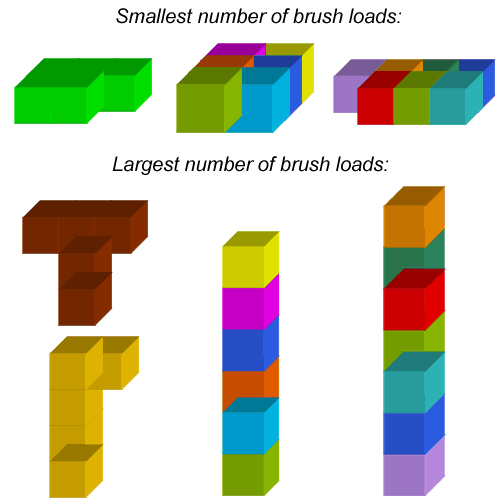
Callum and Josh submitted some ways of making the largest number of brush loads and the smallest number of brush loads for 5, 6 and 7 cubes:
Lan explored the pattern for greater numbers of cubes, as did Rohaan from New Zealand. Lan describes the method used:
From counting cubes, we find:
With 5 cubes, the least number of BLs is 15, and the largest number of BLs is 21.
With 6 cubes, the least number of BLs is 16, and the largest number of BLs is 25.
With 7 cubes, the least number of BLs is 19, and the largest number of BLs is 29.
With 8 cubes, the least number of BLs is 20, and the largest number of BLs is 33.
With 9 cubes, the least number of BLs is 23, and the largest number of BLs is 37.
We remark the pattern:
With 5 cubes, the least number is 15, and the largest number is 21.
With 6 cubes, the least number is 15+1 = 16, and the largest number is 21+4 = 25.
With 7 cubes, the least number is 16+3 = 19, and the largest number is 25+4 = 29.
With 8 cubes, the least number is 19+1 = 20, and the largest number is 29+4 = 33.
With 9 cubes, the least number is 20+3 = 23, and the largest number is 33+4 = 37.
This is interesting, isn't it? If we think about the least number of BLs, we are trying to make as close to a rectangular arrangement of cubes as possible. This helps us to see why we only add one face going from an odd to an even number of cubes, but three faces going from an even to an odd.
However, is a rectangular array always the best for minimising the number of brush loads? If you had 9 cubes, how about making a square arrangement? How many brush loads of paint would you need then?
Ci Hui Minh Ngoc from Kong Hwa School in Singapore worked out the number of brush loads needed for every number of cubes from 1 to 7, thinking particularly about the ways of arranging the cubes to give the smallest and largest numbers of brush loads. Have a look at Ci Hui Minh Ngoc's solution to see if you agree with their ideas. The formula under each diagram represents the number of 'covered' faces, i.e. the number of faces that don't need painting, compared to the total number of faces on each of the cubes.
Ci Hui Minh Ngoc says that when the cubes are arranged in a tall tower, the number of 'covered' faces in the arrangement with n cubes can be written as (n - 1) x 2 + 1, compared to the total number of faces on all of the cubes which would be 6n.
Rohaan's solution says that the largest number of brush loads is always (4 x number of cubes) + 1. Does this tie in with what Ci Hui Minh Ngoc says about the number of covered faces?
Rohaan also worked out that the smallest number of brush loads depends on whether the number of cubes is odd or even:
Odd: (n - 5) x 2 + 15
Even: (n - 6) x 2 + 16
Does this work for a square arrangement too?
Teachers' Resources
Brush Loads
We have five cubes and we're going to join them together, following a few simple rules:
- the cubes must be together face-to-face;
- they must not topple over.
We're going to paint the faces that can be seen. One Brush Load (a kind of unit that we'll use) will paint one square face.
For example, here are five cubes joined together:
Counting the faces to be painted comes to 15, so 15 Brush Loads (or BLs) are needed. Remember we're only counting visible faces, so not those that are touching the surface where the cubes are placed.
But of course we could have placed the five cubes differently, for example:
Counting the faces to be painted now, we have 17, so 17 BLs.
Can you find ways of arranging five cubes so that:
- you need as few BLs as possible?
- you need as many BLs as possible?
Can you find arrangements that need all the numbers between the largest and the smallest numbers of BLs?
What happens if you use more cubes, for example 6, 7, 8...?
Can you find out the smallest number of BLs and the largest number of BLs possible in each case?
Can you predict the arrangements which need as few BLs as possible and as many BLs as possible?
Why do this problem?
This activity is very practical, and encourages visualisation, as well as helping to develop concepts associated with area, particularly surface area. By creating lots of different arrangements of the five cubes, learners will get a feel for ways in which to increase/decrease the surface area and therefore the number of 'Brush Loads'. They can then make conjectures about the largest and smallest possible totals for a different number of cubes, building up to a proof which predicts the results for any number of cubes.
This investigation that can be extended very far indeed, and some pupils may succeed beyond your expectations!
Possible approach
It is worthwhile for pupils to work in pairs or threes and to have cubes in front of them so as to enable productive discussions to take place. As they create different arrangements and work out the number of BLs, listen out for different ways of working and emergent thinking about how to make the number of BLs as large/small as possible. Learners are usually able to articulate that keeping shapes flat produces smaller numbers of BLs and making the tallest towers produces the largest, but challenge them to explain why this is the case. Look out for children moving one cube about from one place to another - you can get into good quality conversations about how many square faces are being covered by the new position and how many new square faces are added.
... they might count "3 plus 3 plus 3 plus 3 plus 8". It then becomes very interesting that with nine cubes there will also be 4 threes but adding 9 at the end. Moving to ten cubes it would be 3 + 4 + 3 + 4 + 10. The discussions can go on and on as pupils' confidence grows.
Key questions
How are you counting the faces?
Are you able to make a shape with more/fewer faces?
Can you explain why or why not?
Possible support
Ensuring that all learners have a supply of cubes and encouraging them to discuss what they are doing will help everyone access this task.
Possible extension
Some learners may move on to tabulating their results. You might want to introduce standard units (cm$^2$) with older children. If you use multilink, 1BL might be equivalent to 4 cm$^2$. Here is a screenshot of a spreadsheet of some findings related to this investigation that you may find useful. But, please don't just hand it out to the children!
You might like to read the article Back to the Practical? which discusses this problem as an example.