Product Sudoku
The clues for this Sudoku are the product of the numbers in adjacent squares.
Problem
Product Sudoku printable worksheet
Product Sudoku printable worksheet for recording your journey
Product Sudoku printable worksheet to see a possible journey
By Henry Kwok

Rules of Product Sudoku
Like a conventional Sudoku, this Product Sudoku has two basic rules:
- Each column, row and $3 \times 3$ subgrid must have the numbers 1 to 9.
- No column, row or subgrid can have two cells with the same number.
The puzzle can be solved with the help of the numbers in the top parts of certain cells. These numbers are the products of the digits in all the cells horizontally and vertically adjacent to the cell.
A Short Demonstration
Getting Started
Alison and Charlie kept a record of the order in which they filled the Sudoku.
They filled the cell marked 1 first, then the cell marked 2, then the cell marked 3...
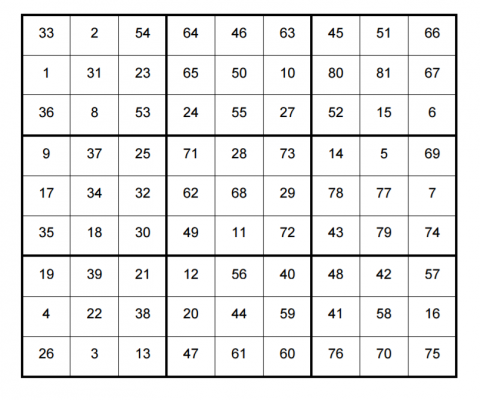
You might like to retrace their route to fill in the cells in the same order, though this is just one possible route through the problem.
You can print their journey here.
Student Solutions
Well done to Agata and Elliot from England, Takuto from Bangkok Patana School in Thailand, Kabir, Arnav P., Arnav B., Nithya, Deethya, Mithravinda, Rivaan, Uday, Udit, Akshobhyan, Srishti, Ruhi, Tejas, Valerie, Nandiinii and Padmini from Ganit Kreeda, Vicharvatika in India, Mason from Irymple Secondary College in Australia, and Mermaid and Frank from Dulwich College Beijing who all sent in correct or nearly correct completed grids. This is Takuto's grid, which is fully correct:
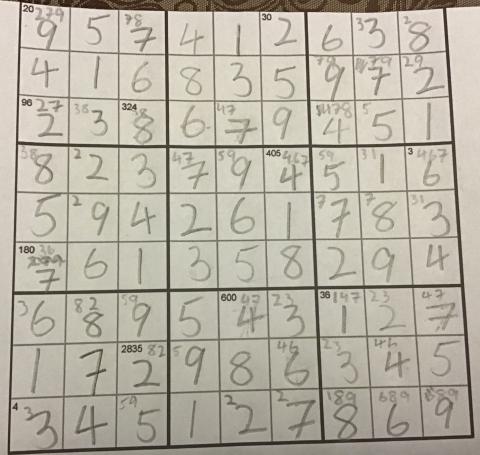
Mason described using different approaches, and finding better methods:
First I started guessing with the factors which now I realise is inefficient and time-consuming if it wasn’t for the help of Julie Powell I would have continued and it would have potentially taken me longer to finish this problem. Julie taught me the importance of factor trees, which sped up the process much faster. I also had times when there were multiple options so I would revert to the definite ones. I then considered squares that overlapped as they limited potential options, it was in them that I began to find my solution. The smaller prime numbers such as 3 were really helpful because they only had one option of 1 $\times$ 1 $\times$ 3. I also realised that the products that had 5 in them would have to have a factor of 5 otherwise it would be impossible to make that product.
Once again, I would like to thank Julie Powell for the few hints and suggestions along the way.
Here are some of Mason's factor trees:

Shubhangee covered the Ganit Kreeda students' journey in tabular form:
Recording of moves is also done. But, it’s not complete. The entries shown in pitch colour are revisited back. This is the overall flow, where I tried to explain each and every move logically.
Now we can solve remaining sudoku using all rules of normal sudoku.
C8 & H9 = 5 (Completed columnwise)
I4 = 1 (Columnwise) & G7 = 1 (Boxwise)
F4=3, B5=3 and A8 = 3 (Tried to put 3 columnwise and boxwise)
After this we were stuck for longer time. But then instead of writing all possible numbers in each cell, we changed our approach. We just wrote wherever we can write 4 for each box. Then we checked for each column and it was clear that for 7th column there is only one place for 4 which is C7.
Then it was pretty smooth to complete the puzzle.
Elliot's journey to complete the product sudoku was different. This is Elliot's work:
- The boxes adjacent to the cell with the 20 in must be a 4 and a 5, because the numbers must be below 10. 5 cannot go below the cell, because 5 is not a factor of 96, so 4 must go below.
- In the bottom left cell with the number 4, the numbers around it have to be a 2 and a 2 or a 4 and a 1. It can’t be a 2 and a 2, because then they’ll be in the same sub-grid, so it must be 1 and 4. The 1 has to go above the cell and the 4 to the side, because if 4 went above there would be two 4s in that column.
- The numbers around the cell with the 3 in have to be 3, 1 and 1 as there are no other numbers that will make 3. The only possible way for them to be arranged to stop the two 1s being in the same sub-grid or column is a 1 next to the 3 cell, a 1 above the 3 cell and the 3 below the 3 cell.
- Then I thought that the only way of making a product of 30 with three whole numbers less than 10 was 2 x 3 x 5 (I realised later this was wrong). I thought the 5 must go below the cell with the 30 because if it were on either side there would be 2 fives in the same row.
- For the 180 in the left column, the only possible combination without having a number over nine or two numbers in the same column is a 5, a 6 and a 6. We can’t put the 5 to the right of the 180 cell because there is already a 5 in that column, which means a 6 has to go there. Then the other 6 cannot go above the 180 cell, because there would be two 6s in the same sub-grid, which means it has to go below the 180 cell and the 5 above it.
- The prime factorisation of 96 is 2^5 x 3. Since there is already a 4 touching the 96 cell, two of the 2s can be ignored, leaving 2^3 x 3. That can be 8 x 3 or 4 x 6. 4 x 6 is impossible without breaking the rules, so it has to be 8 x 3. 8 isn’t a factor of 324, so the 3 has to go there and the 8 below.
- The prime factorisation of 2835 is 3^4 x 5 x 7. The 5 and 7 have to go by themselves, as if multiplied by anything else they will make a number bigger than nine. That leaves 3^4. The only possible combination from that is a 9 and a 9, otherwise it would have to be a 27 and a 3 which wouldn’t work. The two 9s can’t go in the same bottom left sub-grid, which means one has to go to the right of the 2835 cell. The 7 is then the only number which can go to the left of the 2835 and the other 5 and 9 must go above and below, or vice versa.
- The prime factorisation of 405 is 3^4 x 5. The 405 cell is surrounded by 4 cells, which means it has to be split into 4 factors. The two possible ways are 5 x 3 x 3 x 9 OR… 5 x 9 x 9 x 1. The first set of numbers isn’t possible, because of the surrounding 3s, so it must be the second option. The 1 must go below, because of the 1s in the other rows. One of the 9s must be above the 405 cell, because if they weren’t they’d be in the same row, which is impossible. The other two numbers will fill in later.
- A 9 must go in the middle cell of the middle left sub-grid, because it can’t go in the 3rd column because of the 9 mentioned in paragraph 7 and it can’t go in the 4th row down because of the 9 mentioned in paragraph 8. Also, only a 2 can go in the top middle cell of that sub-grid.
- Then I looked at the top left sub-grid. A 9 must go in the 20 cell, because of the 9 that must go above or below the 2835 cell, in the third column, and the 9 already in the third row.
- The prime factorisation of 36 is 2^2 x 3^2. There can’t be a 1 in any of the boxes adjacent to the 36 cell, because of the 1s in the rows and columns around it. So, our solution excludes a 1. Therefore the 4 numbers must be 2, 2, 3 and 3. The number above the 36 cell must be a 2 as there is already a 3 in that sub-grid. The cell below the 36 cell can’t also have a 2, because it would be in the same column, so it must have a 3. A 2 must go to the right, because there is already a 3 in that sub-grid, so the other 3 must go to the left.
- Then, looking at the 30 cell, I realised it couldn’t have a 2 one side and a 3 the other side as I had thought in paragraph 4, because there is already a 2 and a 3 in the right column. It could have a 1 and a 6 instead, with the 6 on the right because there is already a 1 in that sub-grid.
- The prime factorisation of 600 is 2^3 x 3 x 5^2. The 3 is already there, leaving 2^3 x 5^2. The 5s must be alone, because 5x2 would be too big. So there must be two 5s and an 8. One of the 5s must go above and one to the left, because any other combination would not work. That leaves the 3 on the right.
- Once that is worked out, because of the 5 on the left of the 600, we can tell which way around the 9 and 5 mentioned in paragraph 7 go. The 9 is above and the 5 below. Also, because of the 5 above the 600, we can tell which way around the 5 and 9 mentioned in paragraph 8 go. The 9 is to the left and the 5 to the right.
- From there, I thought it was normal sudoku and that I could fill in the rest of the numbers using the normal rules. I started doing that but I got to something which was impossible to make work and realised I must have made a mistake. I couldn’t find the mistake in the steps I wrote above or the normal sudoku (which I didn’t write down all the steps of). I didn’t have time to keep looking for the mistake, so this is as far as I got.
This is what my grid looked like when I started doing normal sudoku at the end of the steps that I wrote out:
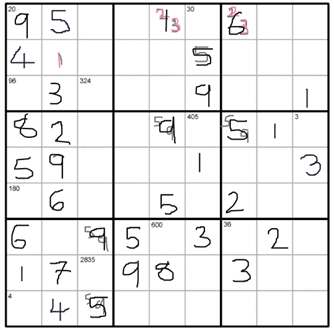
This is what it looked like when I got stuck, when I realised that there was nowhere in the bottom left sub-grid that 3 could go (I used grey for possibilities and black for definites):
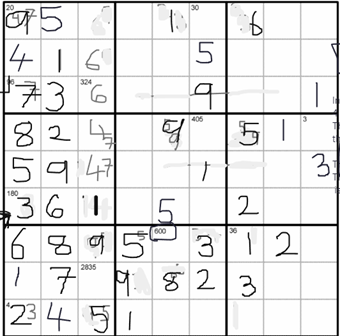
Mermaid and Frank took a similar approach to those above, but used coordinates to label the squares in the grid. As they explained:
First, we assumed that the Sudoku was a coordinate system and each grid in the Sudoku can be shown with coordinates such as (1,2). Thus, each number had its own coordinate for example, the number in the first row and first column is (1,1).
You can see how they used this notation to explain their solution here.
Teachers' Resources
Why do this problem?
This is no ordinary Sudoku because it requires mathematical knowledge in addition to logical thinking. This problem offers an engaging context in which to apply knowledge of factors, multiples and prime factor decomposition.
Possible approach
These printable resources may be useful: Product Sudoku,
Product Sudoku Your Journey,
Product Sudoku a Possible Journey.
If your students do not know the rules of Sudoku then set aside a little time for them to become familiar with the 'standard' Sudoku.
Since this product Sudoku is quite challenging, you may wish to start with A First Product Sudoku and Multiples Sudoku
Display the first one without explaining anything and in silence fill in two adjacent cells.
"I'm going to fill in a few more cells but I'm not going to explain what I'm doing.
If you can work out what I'm doing and can suggest some other numbers then put up your hand.
Please don't spoil it for anyone else by giving away what's happening.
The title of the problem may give you a clue."
Add contributions from the class, in each case asking for a justification, and continue until you feel they have the idea. Provide printed copies for those who wish to complete the problem in their own time and offer them a chance to try Product Doubles Sudoku before they move onto the Product Sudoku.
Offer pairs of students one printed copy of the Product Sudoku and one copy of the blank 9 by 9 grid - the 'journey grid'.
Warn them that this is a little more challenging! On the Sudoku they are going to write the solution. On the journey grid they are going to record the order in which they fill in the cells, from 1-81.You are expecting them to convince each other of the accuracy of their suggestions before anything gets added onto their papers.
When a pair has finished, they put their journey grid on display so that everyone's journeys can be compared. As a plenary, invite comments on any similarities and differences they noticed between their own and others' solutions.
Key questions
Some clues have lots of possibilities and some have few. Which are which?
Which are the most helpful clues to begin?
Possible support
Spend longer on A First Product Sudoku
Provide them with this possible journey through Product Sudoku and suggest they try to retrace the route.
Possible extension
Can one pair take another pair's journey grid and retrace their steps?
