Muggles, Logo and Gradients
Image
|
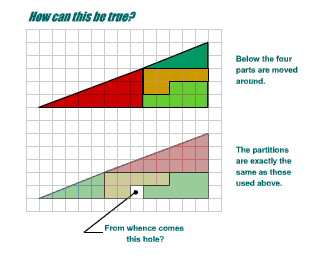
We shall use Logo to throw some mathematical light on the Muggles Magic problem. How can the same four pieces in the jigsaws on the left be placed as shown and leave an extra square hole in the lower arrangement? Look at the diagram on the left, try to explain the 'magic' mathematically for yourself, and then read on.
The Logo programs below show you very accurately the difference in the gradients of the longest sides of the two right angled triangles.
First Forward into Logo is a twelve part introduction to Logo for beginners.
|
Copy the Logo programs you see below on the right, try them out and see what happens.
If you work with the free MSWLogo you can simply copy and paste these programs into the program editor and the same will apply to some other versions of Logo. The lines in the programs starting with a semicolon (;) simply give commentary explaining the programs and they are not an essential part of the programs.
The line joining the point $(0,0)$ to the point $(x,y)$ has slope or gradient $y/x$.
The larger the number $y/x$ the steeper the slope.
If $y/x=1$ then the angle of the slope is $45^\circ$.
If $y/x < 1$ then the angle of the slope is less than $45^\circ$.
If $y/x > 1$ then the angle of the slope is greater than $45^\circ$.
Type the commands below into the Logo command line: SHOW ARCTAN 1 SHOW ARCTAN 5/13 SHOW [ARCTAN 13 5] The first should give $45^\circ$ and the second and third should both give the same angle (a little over $21.8^\circ$). If you have learnt some trigonometry you will recognise the function ARCTAN (often called $tan^{-1}$) which is used here to give the angle of the slope. If you load the programs shown on the right and type: MUGGLES
SLOPE1
what happens?
Yes you get a right angled triangle
with angle of slope ARCTAN 5/13,
because the sides are 650 across and 250 up
(the triangle with sides 13 and 5 enlarged).
Can you see what the scale factor is?
To draw the hypotenuse, the SLOPE1 program
uses Pythagoras Theorem to work out the
length and then multiplies it by the scale factor.
The programs SLOPE2 and SLOPE3
draw the hypotenuses of the two small triangles
in the Muggles jigsaw.
The angles in these triangles are shown by:
SHOW ARCTAN 3/8
SHOW ARC TAN 2/3
and the angle in the large triangle is shown by:
SHOW ARCTAN 5/13
The gradients of the sloping lines are
0.375, 0.4 and 0.385 (to 3 decimal places).
The sequence of programs
MUGGLES
SLOPE1
SLOPE2
SLOPE3
shows the sloping sides of the triangles as
arranged as in the upper jigsaw
and MUGGLES
SLOPE1
SLOPE3
SLOPE2
shows the sloping sides of the triangles as
arranged as in the lower jigsaw.
|
Image
|
TO MUGGLES
CS
;SETPOS places the cursor using coordinates
SETPOS[-200 0]
RT 90
FD 650
LT 90
FD 250
END
TO SLOPE1
;MAKE "A gives a value to the variable :A
MAKE "A 13*13+5*5
MAKE "B SQRT :A
;note the use of Pythagoras Theorem here
PU
SETPOS[-200 0]
PD
RT 90
;(ARCTAN x y) gives the angle whose tangent is y/x
LT (ARCTAN 13 5)
FD 50*:B
;the turtle draws a line with slope y/x
PU
SETPOS[-200 0]
PD
RT (ARCTAN 13 5)
;now the turtle points in the x direction
END
TO SLOPE2
MAKE "A 3*3+8*8
MAKE "B SQRT :A
LT (ARCTAN 8 3)
FD 50*:B
RT (ARCTAN 8 3)
END
TO SLOPE3
MAKE "A 2*2+5*5
MAKE "B SQRT :A
LT (ARCTAN 5 2)
FD 50*:B
RT (ARCTAN 5 2)
END
|
The Logo drawings show you that, what at first sight look like two right-angled triangles with sides $13$ and $5$, are in fact two quadrilaterals. One is just half a unit in area smaller than the triangle and the other one is just half a unit in area bigger. The Logo program shows you how close these two quadrilaterals are to the right-angled triangle.