Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
Problem
Triangle Midpoints printable sheet
Given the three midpoints of the sides of a triangle, can you find a way to construct the original triangle?
For example:
Choose any three points.
Can you construct a triangle such that your three points are the midpoints of its sides?
Is there more than one possible triangle for any given set of midpoints?
Getting Started
Draw any triangle, find the midpoints, and join them.
What do you notice?
How can this help you solve the problem in reverse, starting with the midpoints and constructing the triangle?
Student Solutions
We received different approaches to the solution. The first is based on what Stephanie from Beecroft School noticed.
Stephanie noticed that the large triangle is made from four congruent triangles, one of which is the triangle joining the midpoints. Stephanie therefore created the larger triangle by making three copies of the smaller one and translated and rotated them into place.
My question is:
How do you know the triangles are congruent? Does the following diagram help?
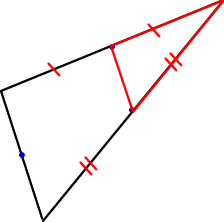
Chip at King's Ely School and Eli sent in a solution based on Stephanie's ideas.
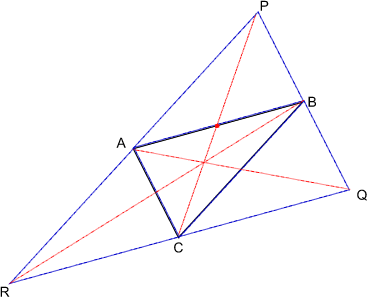
Like my question above, I want to know how you know the vertices of the larger triangle can be found in this way? Also, if you can convince me you are right, how does the construction to find the midpoint of the sides of the triangle work and why?
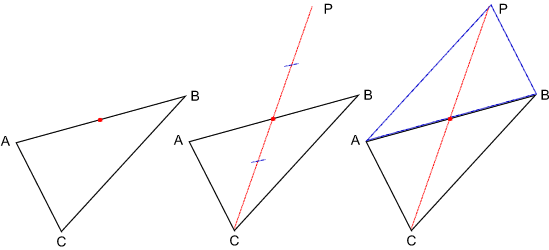
The second approach involved parallel lines:
The original triangle PQR can be drawn by constructing a line through A parallel to BC, a line through B parallel to AC and a line through C parallel to AB.
You should then be able to prove that the points A, B and C are the mid-points of PR, PQ and QR.
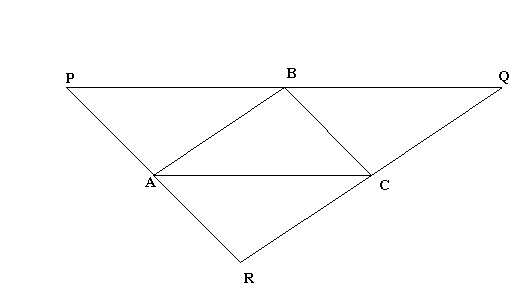
How do you know the sides of the larger triangle are parallel and how can you construct each of the lines parallel to the sides of the original triangle. Why does the construction work?
We asked you to tell us more about how these ideas work.
Shu Qian Yang suggested the following approach, which tells us more about constructing the parallel lines.

Starting with triangle ABC, Shu Qian Yang used a protractor to help him draw two new lines. As he explains, he first constructed a line perpendicular to AC.
I can use a protractor to measure $90^{\circ}$ on top of point A, then plot N as the $90^{\circ}$ point. Afterwards, I connect point A and N with a dotted line. Now we have a perpendicular line called AN.
He then uses the protractor again to construct a line perpendicular to AN, which will be parallel to AC.
Next, on AN, I would again measure $90^{\circ}$ and name it point Z. But point Z should level with point B. Then I connect point Z with point B. Now two perpendicular lines make a pair of parallel lines.
In the next step Shu Qian Yang uses the idea that B is the midpoint of the original triangle's side. He uses this to construct a line with endpoints P and Q so that PQ is in line with the line ZB and B is its midpoint. He explains how he used this to construct the rest of the triangle, with third vertex R.
For RQ, I connect Q with C and double this length, because AB is half RQ. I can draw the last line without any calculations. The construction works because after I use the parallel lines, I get a larger triangle with its mid-points.
This approach justifies how to construct the line PQ parallel to AC, and to use this to construct a triangle, but it still leaves us wondering why the sides of the original triangle are parallel to the sides of the triangle of midpoints. We'd still like to hear more about why these sides should be parallel. Please email us if you've got any ideas about this.
Teachers' Resources
Why do this problem ?
Possible approach:
To start with there is some thinking to do about the way in which knowledge of the mid points is sufficient to fix the triangle (which may be surprising). Show the question and ask for ideas about possible approaches, things students notice and things that might be true but they/others would need to be convinced about.
- What does it look like?
- Is it regular?
- Ask students what they notice? The answer might just be that they make a triangle but press for any other ideas which might emerge that you could pursue.
Use time to discuss what different groups notice and how it might help. Encourage students to make careful arguments to help them to work rigorously.
This problem creates a good opportunity to practise some common classroom geometry constructions, for example: a perpendicular bisector of a given line, angle bisector, centre for the circumcircle of a given triangle, drawing a line through a given point parallel to a given line.
It is particularly important to promote a lively discussion of possible reasons for a construction method's validity.
Key questions:
- What does working backwards from what you know reveal about the problem that could be helpful?
- How do you know...? How can you convince us?
- Why does the construction work ?
Possible support:
Establish the relationships with paper folding and cutting and use this to see why triangles are congruent and therefore why particular approaches are valid.
