Witch of Agnesi
Sketch the members of the family of graphs given by $y = a^3/(x^2+a^2)$ for $a=1, 2$ and $3$.
Problem
Sketch the members of the family of graphs given by $$y = {a^3\over (x^2+a^2)}$$ for $a=1$, $2$ and $3$.

Getting Started
Consider symmetry.
Find the critical values (turning points).
Consider what happens to the graphs for large $x$ (possitive and negative) and hence find the asymptote.
Student Solutions
Sanjeet sent us this graph, showing the three curves on the same graph:
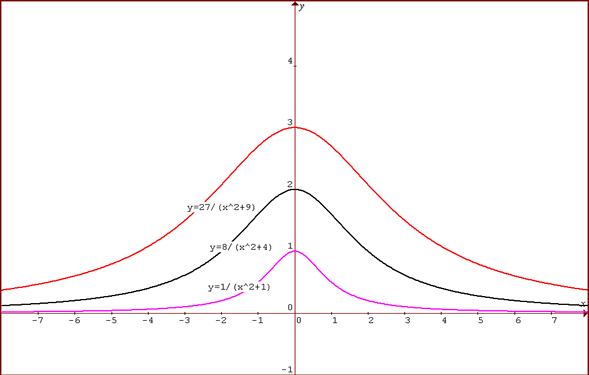
For different values of $a$ the graphs have the equation: $$y = {a^3\over (x^2+a^2)}$$ Differentiating $${dy\over dx} = - {2a^3x\over (x^2+a^2)^2}.$$ So the critical value is at $(0,a)$. Near this point, for small negative $x$ the gradient is positive and the function increasing and for small positive $x$ the gradient is negative and the function decreasing so this is a maximum point.
The value of $y$ is always positive so the entire graph lies above the $x$ axis and the graph is symmetrical about $x=0$ because $f(-x)=f(x)$.
For large $x$ the value of $y$ tends to zero so the line $y=0$ is an asymptote.
Teachers' Resources
Why do this problem?
The problem gives practice in the usual techniques for curve sketching (considering symmetry, finding turning points, looking for asymptotes). It also introduces the idea of a family of curves.
Possible approach
Suggest different members of the class sketch the different graphs (for $a=1$, $2$ and $3$). Have a class discussion about the results they find.
Key questions
Will the graphs have a similar shape for all values of $a$?
What about negative values of $a$?
Possible extension
If the class can differentiate simple functions defined parametrically or implicitly then they could also try: Squareness and Folium of Descartes.
