Olympic Magic
in how many ways can you place the numbers 1, 2, 3 … 9 in the nine regions of the Olympic Emblem (5 overlapping circles) so that the amount in each ring is the same?
Problem
The Olympic emblem consists of five coloured rings which overlap to give nine regions. Here is a black and white diagram showing the overlaps:

In order to contribute to a pension fund for the retiring International Olympic Committee people are asked to deposit money into each region.
The guidelines allow the delegate to take all the money in any one of the rings.
Place the numbers 1, 2, ... 9 in the nine regions so that the amount in each ring is the same. How many different ways can you find to do this?
(Problem from University of Sydney Mathematics Enrichment Groups 1999)
Getting Started
The four overlapping regions could be edges in a graph and the remaining regions vertices. Each vertex and each edge has a unique number assigned to it. This is a problem on vertex magic graphs! A graph is vertex magic if, for each vertex, we get the same magic sum when we add the number at that vertex to the numbers on all the edges joined to that vertex.
What is the grand total of the sums at the 5 vertices? The numbers on the edges are counted twice so add this to the total of the numbers 1 to 8. What does this tell you about the total of the numbers on the edges (that is in the overlapping regions)? This gives you information about the possible values for the magic sum.
Be systematic and you?ll be able to check all the possibilities. What pairs of numbers can you use in the outer circles? What numbers can you then use in the overlapping regions (the edges of the graph).
There are several solutions. How will you know when you have found them all?
Student Solutions
Thank you to Alma Iulia Dimitriu, of St Peter's RC High School, and member of the NRICH/NAGTY mentoring scheme), for this solution.
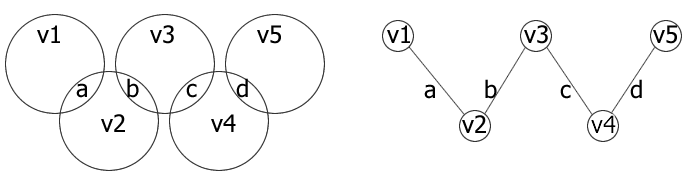
We are working here with vertex magic graphs.
When we draw a graph for the problem there are 5 vertices and 4 edges. A vertex sum is the sum of the numbers on the vertex and on the edges joined to that vertex. The sum in each circle (which can be either 10,11,12,13,14 or15) is the vertex sum in the graph and we want to make this a constant X to make it a magic sum.
The sum of all the numbers is: 1+2+3+4+5+6+7+8+9 = 45
The edges are used twice. There are 4 numbers included in two circles and the sum of the 4 edges that are used twice is a+b+c+d=n, so n + 45 = 5X. So n has to be multiple of 5.
Also 1+2+3+4 = 10 so X must be greater than or equal to 10. So which means that 10 cannot be the magic sum.
For X to be 15, n has to be 30 and the only 4 numbers that add up to 30 are 6+7+8+9. It is impossible for any of them to be on the edges because the only pairs of numbers that add up to 15 are 9+6 and 7+8 and two of these numbers have to be placed at the two outer vertices.
For X to be 12, n has to be 15. There can be 3 pairs of numbers that equal 15, that is 10+5; 9+6 and 8+7. There are 4 numbers to make n because there are 4 edges. So all the possible choices of the 4 numbers on the edges are:
|
The only two numbers that equal 12 (for the 2 circles on the margins) are: 9+3; 8+4 and 7+5.
So v1 and v5 have to be any two of those numbers. So now the possibilities left for the edges are:
For 10+5:
1+9+2+3 - no solution as the only two numbers here are 3+9=12 (they can't be separated)
2+8+4+1 - no solution the same as above
3+7+4+1 - a possible solution because for v1=7 and v5=4
4+6+2+3 - no solution
For 9+6: - no solutions
For 8+7: 1+7+3+4 (the same as the one above)
So now we only have two possible solutions where 7 and 4 have to be on the margins:
Case (i) a=4, b=1, c=3, d=7
a=4 needs v1=8 to make 12. The second circle already has 4 and 1 so it will need v2=7 to make 12. This cannot be a solution because we already have d=7.
Case (ii) a=7, b=1, c=3, d=4
a=7 will need v1=5 to make 12. The second circle has 7 and 1 and it will need v2=4 but this is impossible as d=4.
So there is no possible solution with X equal to10, 12 or 15
The remaining values for X are 11, 13 and 14 for which 5X=55, 65 and 70. As n + 45 = 5X we have n=10, 20 and 25.
For X=11, the only numbers for the edges to add up to 10 are: 1+2+3+4 and the only pairs to make 11 are: 9+2, 8+3, 7+4 and 6+5. Checking all the possible cases gives the following solution and its mirror image:
v1=8, a=3, v2=7, b=1, v3=6, c=4, v4=5, d=2, v5=9
For X=13 we have a+b+c+d=n=20 and checking all possible cases gives two solutions and their mirror images;
v1=9, a=4, v2=1, b=8, v3=3, c=2, v4=5, d=6, v5=7
v1=4, a=9, v2=1, b=3, v3=8, c=2, v4=5, d=6, v5=7
For X=14 we have a+b+c+d=n=25 and one solution with its mirror image
v1=5, a=9, v2=2, b=3, v3=4, c=7, v4=1, d=6, v5=8
Teachers' Resources
Why do this problem?
In this problem learners have to identify the mathematical features of the context and represent these features in graphical and algebraic forms. They will get practice in analysing and mathematical reasoning through using algebraic expressions and equations to find solutions. In order to check that they have found all possible solutions learners need to work systematically and check all possible cases.
Key questions
What is the sum of the whole numbers 1 to 9?
If the total in each circle is X, what can you say about the total of the numbers that are in the intersections of the circles?
