Folium of Descartes
Investigate the family of graphs given by the equation x^3+y^3=3axy for different values of the constant a.
Problem
Investigate the family of graphs given by the equation
$$x ^3+y^3=3axy$$
for different values of the constant $a$.
It is more of a challenge to try to sketch the graphs with the ideas explored in this question without graphing software but you may like to use it if you have software that plots the graphs of implicit functions or parametric functions.
Prove that the graphs are all symmetrical about the line $y=x$.
Make the substitution $y=tx$ to express the equation in parametric form $(x,y)=(f(t),g(t))$.
Show that all the graphs have a maximum point when $t=2^{1/3}$ and find the coordinates of the maximum point.
Show that:
a) for $-\infty< t< -1$ the graphs lies in the fourth quadrant with $x$ positive and $y$ negative
b) for $-1< t< 0$ the graphs lie in the second quadrant with $x$ negative and $y$ positive
c) for $0< t< 1$ the graphs lie in the first quadrant with $0< y< x$
d) for $1< t< +\infty$ the graphs lie in the first quadrant with $0< x< y$.
What happens to the graphs for $t=-1$?
Getting Started
Invistigate symmetry by exchanging $x$ and $y$ in the equation of the graph.
The question itself gives you guidance as to the methods to use.
Student Solutions
This excellent solution came from Marcos from Cyprus.
As I don't have any graphing software I'll be using the ideas in the question to sketch the graph at the end. I will try to give as detailed explanations as I can.
I'm assuming the constant $a$ is positive.
Firstly we show that the graph is symmetrical about $y=x$. How do we know if a graph is symmetrical about $y=x$? One simple approach is, if we change the $x-$ and $y-$axes round and plot it again we should get the graph looking as it did in the original case.
(To see this better, think of what happens when you 'fold' the $x-y$ plane along $y=x$).
Therefore, since we can swap the axes and preserve the shape this implies that we can just check if in our equation we can replace the $x$ with $y$ and the $y$ with $x$ and still get the same graph. This is obviously true:
$$x^3+y^3=3axy$$ goes to $$y^3+x^3=3ayx$$
which is the same thing. Thus, the graphs are symmetrical about $y=x$.
Using $y=tx$ in the equation, we get:
$$x^3 + t^3x^3 = 3atx^2.$$
When $x\neq 0$ and $t\neq -1$ we can divide by $x^2$ and $1+t^3$ and get
$$x={3at\over {1+t^3}},\quad y={3at^2\over {1+t^3}}.$$
To find a maximum point we can differentiate using the chain rule wrt $x$:
$$3x^2+3y^2{dy \over dx} = 3ay + 3ax{dy\over dx}.$$
Hence $${dy\over dx}= {{ay-x^2}\over{y^2-3a}}.$$
Now, the maximum is when $dy/dx = 0$, that is when $ay = x^2$. Using $y=tx$ gives $atx = x^2$ and when $x\neq 0$ this is at $x = 3at/(1 + t^3)$ so $1 + t^3 = 3$ and thus $t=2^{1/3}$ at the stationary point. Looking at the parametric form, this occurs at the point $(2^{1/3}a, 2^{2/3}a)$. Putting in an x-value just before and just after confirms the point to be a maximum.
(a) When $t$ is in $-\infty< t< -1$ from the parametric form of the equation $x$ must be positive and $y$ must be negative.
(b) When $t$ is in $-1< t< 0$ then $x$ is negative and $y$ must be positive.
(c) When $t$ is in $0< t< 1$ then $3at > 0$ and $t^3 > 0$ so $x$ is positive and so is $y$ but as $y = tx$ then $y < x$.
(d) Similarly when $t > 1$, $3at > 0$ and $1 + t^3> 0$ and so $x$ and $y$ are positive. As $y = tx$ then $x< y$.
For $t=-1$ the graph is undefined but as $t$ tends to -1 the absolute values of $x$ and $y$ get larger and the graphs get closer and closer to the asymptote $y = -x$.
One last aid to sketching the curve is the following. Is there a point such that $y=x$? Considering our equation, $2x^3=3ax^2$ at such a point. We already know (0,0) is on the graph so for other points we can divide by $x^2$. We get $x = y = 3a/2$ which corresponds to $t=1$. The important thing about this point is that considering our formula for $dy/dx$ if $x = y$ then $dy/dx = -1$ and so we know that at this point the gradient is that of the line $y = -x$. This tells us that (as the curve is symmetrical about $y = x$ and using parts (c) and (d) there is a 'loop' at this point.
Using all of this information, we conclude that a sketch of the graph looks something like this:
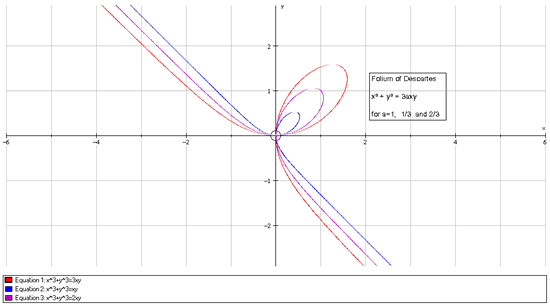
Teachers' Resources
Why do this problem?
The problem gives experience of investigating curves, considering properties like symmetry, making substitutions to give the parametric equation of the curve, and conversion between Cartesian and parametric forms.
Differentiation of the parametric form and the use of the Chain Rule is required to find the turning points.
Detailed guidance is given (scaffolding) to support the learner in working through the problem.
Possible approach
To encourage independent learning, learners could work in pairs to discuss and follow the steps in the problem. If they are stuck the teacher could indicate which part of the guidance given in the question itself might help them.
At some point a class discussion could be used to review the process and to make sure all the learners can understand and complete it. In this review the teacher can point out that the steps are similar for investigating other curves.
Key questions
See the scaffolding given in the question itself.
Consider how the two Cartesian graphs $x=f(t)$ and $y=g(t)$ can give insight into the shape of the parametric graph $x=f(t)$, $y=g(t)$. Can you use this to visualise how the graph unfolds as $t$ increases from $0$?
Possible support
The question Witch of Agnesi is a little easier and might be tackled first.
Possible extension
Squareness is another graph sketching problem on the family of relations: $x^n + y^n = 1$ where the curves have different forms for odd and even values of $n$.
