Instant Insanity
Given the nets of 4 cubes with the faces coloured in 4 colours, build a tower so that on each vertical wall no colour is repeated, that is all 4 colours appear.
Problem
These are the nets of 4 cubes. Build a tower so that on each vertical wall no colour is repeated, that is all 4 colours appear.
Image
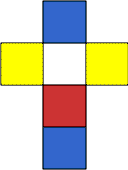
| Image
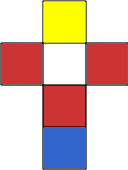
| Image
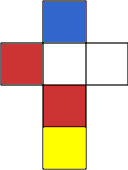
| Image
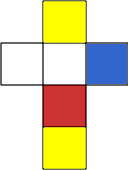
|
Printable NRICH Roadshow resources.
Getting Started
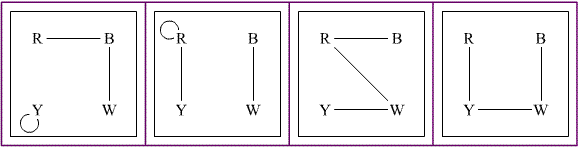
The edges in these 4 graphs show the colour pairings of opposite faces of the cubes.
To solve the problem combine all 4 graphs then look for 2 subgraphs, one representing the colours on the front and back walls of the tower and the other representing the colours on the left and right hand walls of the tower, such that each contains all 4 colours and precisely one edge of each numbered cube.
Student Solutions
This solution is from Shu Cao of the Oxford High School for Girls. Well done Shu!
Let B=blue, W=white, Y=yellow and R=red.
The colours of the walls of the tower listed from top to bottom in columns 1-4 are:
|
One can swap the columns 1234 to create 4X3X2X1=24 different towers.
Method:
|
The tower has 4 walls so each colour only appears 4 times on the walls. There are 7 red, 6 yellow, 6 white and 5 blue so 3 red, 2 yellow, 2 white and 1 blue will be either within the tower or directly on the top and bottom of the tower.
Incidentally, there are 3 red flaps, 2 yellow flaps, 2 white flaps and 1 blue flap in line 2. Assuming that they can be folded over into the tower or onto the top and bottom, the faces left in columns 1234 will make up the walls of the tower.
All that one has to do now is to move the columns up and down so as to line different colours together. Line up 1 and 2 first, when there is a protruding flap, move it onto the top or bottom of the column depending on circumstances. Proceed to columns 3 and 4 in the same way.
Another method is to use graphs. The edges in the graphs below join the colours that appear on opposite faces of the cubes.
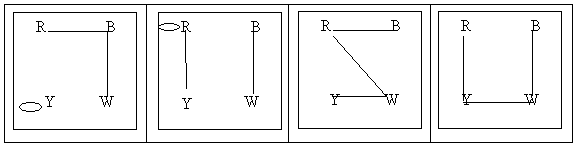
To solve the problem next combine all 4 graphs, writing 1, 2, 3, and 4 on the edges denoting which of the 4 cubes they represent. Then look for 2 subgraphs, in this case two square circuits chosen from combined graph, such that each contains all 4 colours and precisely one edge of each numbered cube. One subgraph will represent the colours on the front and back walls of the tower and the other subgraph will represent the colours on the left and right hand walls of the tower.
If you can draw the combined graph and the two subgraphs giving the solutions then do send them in for publishing with this solution.
