Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Odds and Evens
Age 11 to 14
Challenge Level 





Odds and Evens printable sheet
Here is a set of numbered balls used for a game:
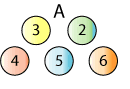
To play the game, the balls are mixed up and two balls are randomly picked out together. For example:

The numbers on the balls are added together: $4 + 5 = 9$
If the total is even, you win.
If the total is odd, you lose.
How can you decide whether the game is fair?
You might like to experiment with the interactivity below.
Here are three more sets of balls:
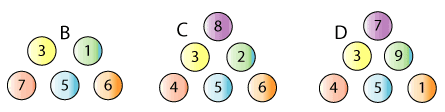
Which set would you choose to play with, to maximise your chances of winning?
Click on the links below to explore each set using the interactivity.
What proportion of the time would you expect to win each game?
You may wish to look at the problem Odds and Evens Made Fair to explore whether it is possible to change the number of balls to make the game fair.