Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Odds and Evens
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Alfie from Tain Royal Academy in Scotland used the interactvity to test whether the game is fair with set A:
I'm going to take a total sum of wins for every hundred rolls up to 500 rolls:
100 rolls -42 wins (relatively fair random results, the closer to 50 it is the more fair it is)
200 rolls- 88 wins (still 12 wins from exactly fair)
300 rolls- 133 wins (a bit further than last time)
400 rolls- 169 wins (straying further from 50/50 split)
500 rolls- 207 wins (almost 50 wins from fair)
Now I'll jump to 1000 rolls- 416 wins (still 84 wins from an even 500)
From this I can conclude that from 100 rolls the results are slowly dropping from the even split. From here I can say with almost certainty that it is not quite fair”ƒ
Scout from Jmes Allen Girls School used the same strategy for sets B, C and D:
Set B
The mean of winning when I played 100 times:
0.570, 0.500, 0.640, 0.600, 0.560
Overall mean: 0.574
Set C
The mean of winning when I played 100 times:
0.460, 0.470, 0.420, 0.480, 0.440
Overall mean: 0.454
Set D:
The mean of winning when I played 100 times:
0.690, 0.670, 0.590, 0.630, 0.670
Overall mean: 0.650
I would probably play with D to make sure I had the most chance of winning.
Scout also looked at set A in more detail:
I worked out the many possibilities for Set A:
Please note: W=win L=lose and each combination is in inverse (e.g. 2 + 3 and 3 + 2 are both listed here)
2+3=5=L
2+4=6=W
2+5=7=L
2+6=8=W
We notice a pattern as we go systematically through them, as we increase the last number we are adding by 1, it goes through a multitude of odd, even, odd, even etc.
3+2=5=L
3+4=7=L
3+5=8=W
3+6=9=L
Here, because 3 is an odd number there are three loses and a win instead of an equal number of each set.
4+2=6=W
4+3=7=L
4+4=8=W
4+5=9=L
An equal number on the sets. It seems like on an even is equal. This makes sense as an odd add an even is an odd and an odd add an even is an odd too. This means it is higher probability of you getting an odd result.
5+2=7=L
5+3=8=W
5+4=9=L
5+6=11=L
Already, we can see the probability is higher to get an odd result than an even one by a long shot.
6+2=8=W
6+3=9=L
6+4=10=W
6+5=11=L
Again, an equal number.
Daniele from Southlands International School, Rome in Italy, Ali from Garden International School in Malaysia and Mahdi from Mahatma Ghandi International School in India also listed the probabilities, and counted up the number of winning combinations. Ali wrote:
The game is not fair because with the set of different 5 balls there are 10 possible number combinations (Ali does not list the combinations that Scout described as "inverse", so has 10 instead of 20)
When I checked there are 6 answers which are odd and 4 answers which are even. Therefore, there is a 60% chance you will get an odd number and a 40% chance you will get an even number.
Daniele also made lists of all of the possibilities for sets B, C and D:
If I want to maximise my chances of winning, I would choose set D.
Set 8B from Manchester High School for Girls used tables to show all of the possible combinations for all of the sets:
From the table we have worked out all the possible outcomes of the experiment. We have ignored the diagonals as we are choosing numbers without replacement.
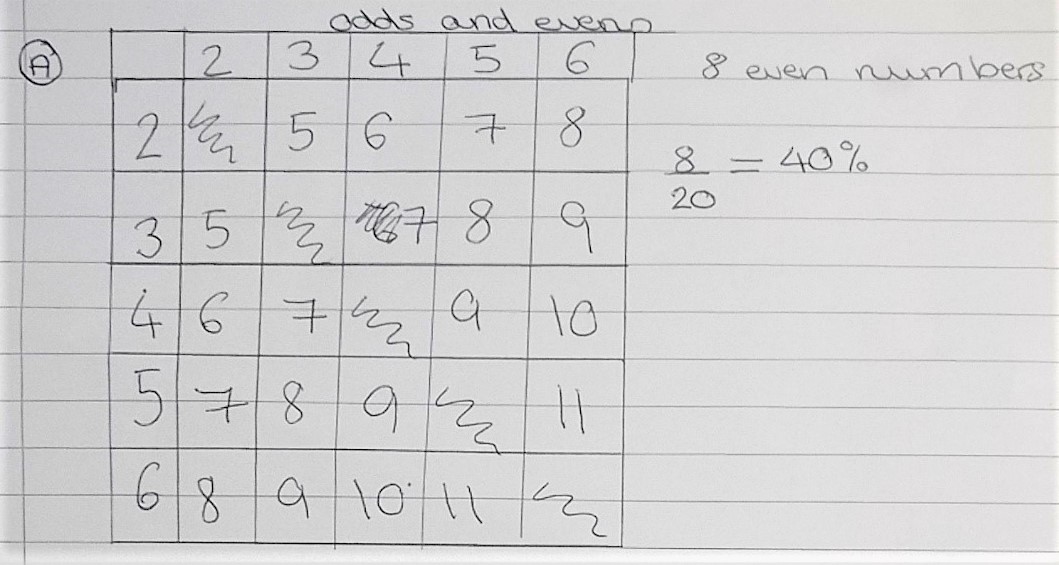
One group noticed that we only needed to use half of the table to work out the probabilities as the table is mirrored about the diagonal. Using a similar table for set B, we can see that there are 6 evens out of a possible 10. Therefore, the probability of winning is 60%.
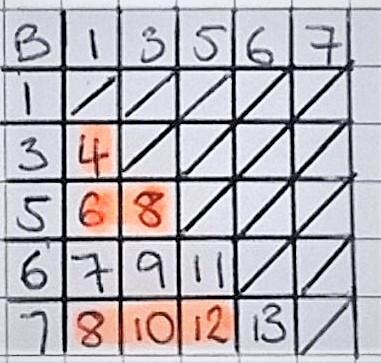
Using a similar method, we found out what all the outcomes were using set C. From this we can see that there are 14 even outcomes and 16 odd outcomes. Therefore, we have 14 winning outcomes out of a possible 30 and so the probability of winning is 46.7%.
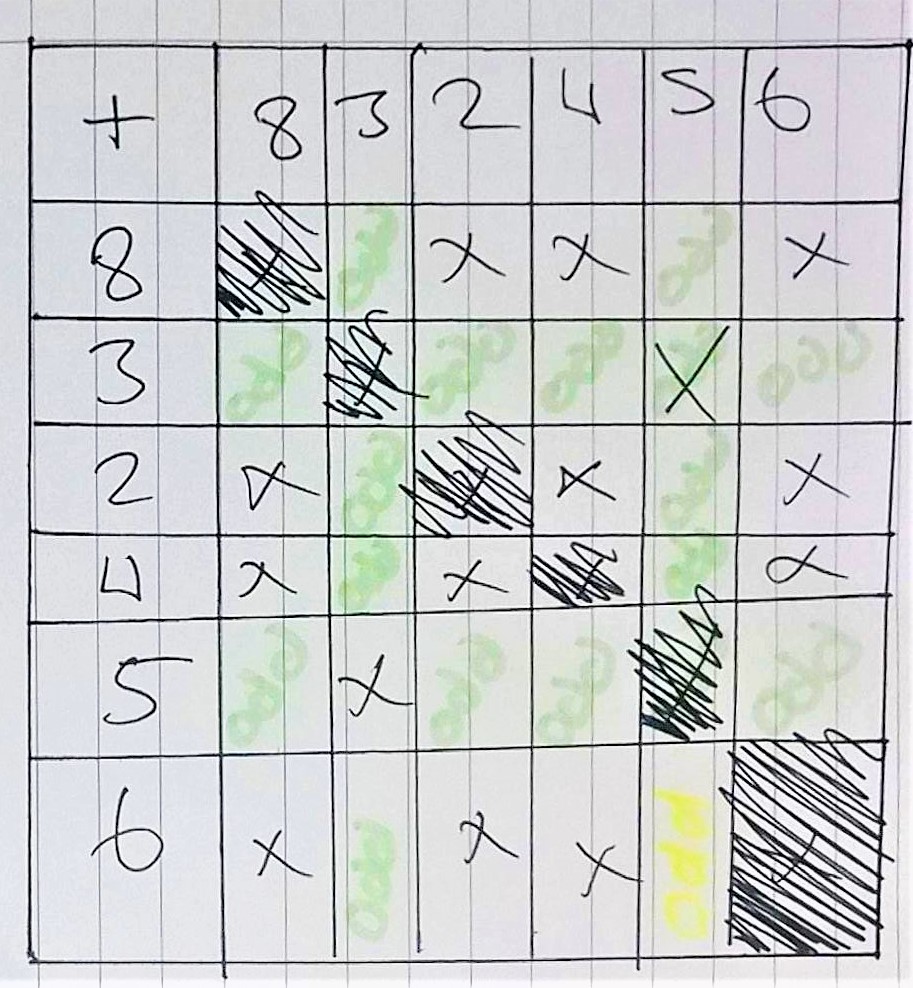
Below is a table representing the sample space diagram for set D. From here we can see that there are 20 even outcomes and 10 odd outcomes. Therefore, we have 20 winning outcomes from a possible 30 and so the probability of winning is 66.7%.

Overall, as set D gives us the greatest probability of winning, we would choose to play with set D to maximise the chances of winning.
Sanika P from PSBBMS, OMR in India used tree diagrams to represent the possibilities for each set:
Set A
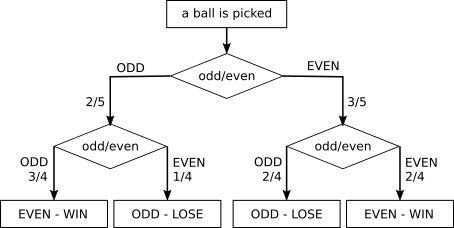
Probability of Odd-Odd combination $ = \frac25\times\frac14 = \frac2/{20}$
Probability of Even-Even combination $ = \frac35\times\frac24 = \frac6{20}$
Total chance of winning $ = \frac2{20}+\frac6{20} = \frac8{20} = 0.4 = 40\%$
Set B
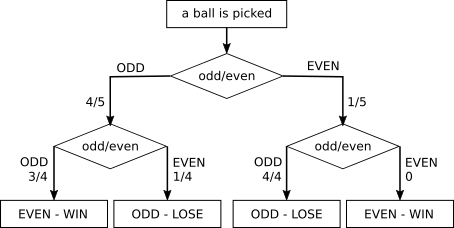
Probability of Odd-Odd combination $ = \frac45\times\frac34 = \frac35$
Probability of Even-Even combination $ = \frac15\times0 = 0$
Total chance of winning $ = \frac35+0 = \frac35 = 0.6 = 60\%$
Set C
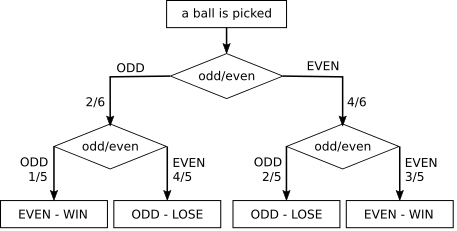
Probability of Odd-Odd combination $ = \frac26\times\frac15 = \frac2{30}$
Probability of Even-Even combination $ = \frac46\times35 = \frac{12}{30}$
Total chance of winning $ = \frac2{30} + \frac{12}{30} = \frac{14}{30} = 0.467 = 46.7\%$
Set D
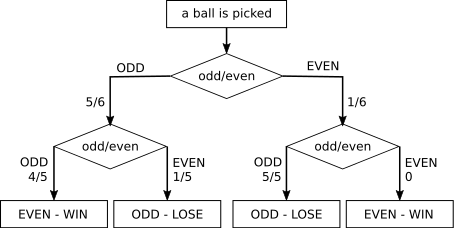
Probability of Odd-Odd combination $ = \frac56\times\frac45 = \frac{20}{30} = \frac23$
Probability of Even-Even combination $ = \frac16\times0 = 0$
Total chance of winning $ = \frac23+0 = \frac23 = 0.667 = 66.7\%$
Maria Ester from Italy used a similar method but didn't draw the whole trees. This is Maria Ester's work:

Tom and Hussein from Wilson's School and Daniele found the same set that produced a fair game:
To produce a fair set of numbers from what we found out you would need 4 balls, one odd and three even, or the other way round, one even and three odd.
Daniele also found that these sets would give a fair game:
Mahdi used the notation $\left(\begin{matrix}n\\2\\ \end{matrix}\right)$, where $\left(\begin{matrix}n\\2\\ \end{matrix}\right)$ is the number of ways of choosing $2$ balls from a set of $n$ balls.
For any general set containing $o$ odd numbers and $e$ even numbers
Total number of pairs formed $ = \left(\begin{matrix}o+e\\2\\ \end{matrix}\right)$
Total favourable pairs can be formed by choosing pairs of odd numbers and pairs of even numbers
Number of favourable outcomes $ = \left(\begin{matrix}o\\2\\ \end{matrix}\right) + \left(\begin{matrix}e\\2\\ \end{matrix}\right)$
Probability $= \dfrac{\left(\begin{matrix}o\\2\\ \end{matrix}\right)+\left(\begin{matrix}e\\2\\ \end{matrix}\right)}{\left(\begin{matrix}o+e\\2\\ \end{matrix}\right)}$
Let us verify the general strategy for set A, set B, set C and set D
For set A, 2 odd, 3 even: $= \dfrac{\left(\begin{matrix}2\\2\\ \end{matrix}\right)+\left(\begin{matrix}3\\2\\ \end{matrix}\right)}{\left(\begin{matrix}5\\2\\ \end{matrix}\right)} = \dfrac{1+3}{10} = \dfrac4{10}$
For set B, 4 odd, 1 even: $= \dfrac{\left(\begin{matrix}4\\2\\ \end{matrix}\right)+\left(\begin{matrix}1\\2\\ \end{matrix}\right)}{\left(\begin{matrix}5\\2\\ \end{matrix}\right)} = \dfrac{6+0}{10} = \dfrac6{10}$
For set C, 2 odd, 4 even: $= \dfrac{\left(\begin{matrix}2\\2\\ \end{matrix}\right)+\left(\begin{matrix}4\\2\\ \end{matrix}\right)}{\left(\begin{matrix}6\\2\\ \end{matrix}\right)} = \dfrac{1+6}{15} = \dfrac7{15}$
For set D, 5 odd, 1 even: $= \dfrac{\left(\begin{matrix}5\\2\\ \end{matrix}\right)+\left(\begin{matrix}1\\2\\ \end{matrix}\right)}{\left(\begin{matrix}6\\2\\ \end{matrix}\right)} = \dfrac{10+0}{15} = \dfrac{10}{15}$

