Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Odds and Evens



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem offers an opportunity to explore and discuss two types of probability: experimental and theoretical. The simulation generates lots of experimental data quickly, freeing time to focus on predictions, analysis and justifications. Calculating the theoretical probabilities provides a motivation for using sample space diagrams or perhaps tree diagrams.
Possible approach
You may wish to use the start of What Numbers Can We Make? as a preliminary activity to get students thinking about the effect of combining odd and even numbers.
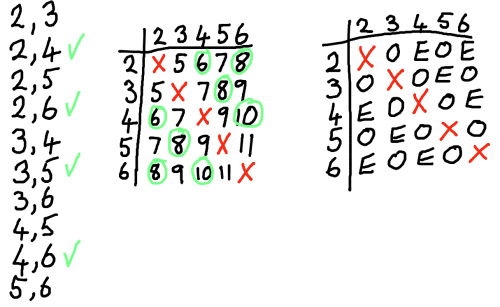
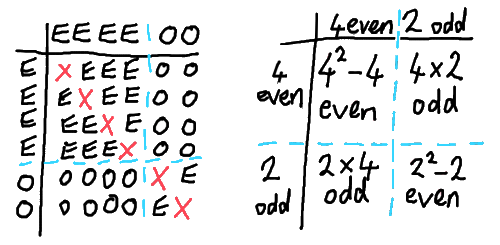
Key questions
How can you decide if a game is fair?
Possible support
Flippin' Discs could be used as a simpler context for exploring theoretical and experimental probability.
Possible extension
The problem In a Box offers another context for exploring exactly the same underlying mathematical structure, and could be used as a follow-up problem a few weeks after working on this one.

