30-60-90 Polypuzzle
Problem

Can you re-arrange the pieces of the puzzle to form a rectangle by sliding the pieces without rotating them? Now can you re-arrange the pieces to form an equilateral triangle by flipping the pieces numbered $2$ and $5$ and moving them into new positions?
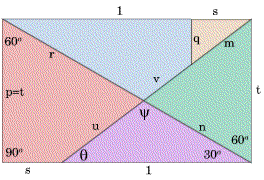
You can assume that pieces $1$ and $5$ each have a side of length one unit, that the pieces as shown form a perfect square of area one square unit and that they do fit together to form a perfect equilateral triangle of the same area.
Calculate the length $t$ of the edge of piece $3$ and then calculate the lengths of all the other edges giving answers correct to $3$ significant figures. You can use the interactivity below to explore how the pieces fit together.
Getting Started
Finding the lengths depends on using the ratio for the sides of a 30-60-90 triangle as the name of the problem suggests. Below the diagrams show how to take the pieces which make a square of unit area and fit the pieces together to make an equilateral triangle of the same area with side $2t$ and knowing this you can calculate $t$. The way pieces fit together gives you that $p=t$ and the rest is up to you!
You can calculate the length '$t$' knowing the area of the equilateral triangle. Pythagoras theorem and the sine rule can be used in finding the other lengths.
Student Solutions
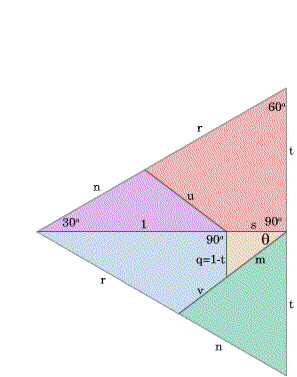
Teresa solved this problem, using this hints we gave:
The area of the equilateral triangle is $1=\frac{1}{2}\times(2t)^2\times\sin 60^{\circ}$ so $t^2=\frac{1}{\sqrt{3}}$, so $t=\frac{1}{\sqrt[4]{3}}\approx 0.760$.
We know that $p=t$ and $q=1-t$, so $p\approx 0.760$ and $q\approx 0.240$.
The height of the equilateral triangle is $1+s=t\sqrt{3}$ so $s\approx 0.316$.
We can use Pythagoras' Theorem to find $m$: $m^2=s^2+(1-t)^2\approx 0.156$, so $m\approx 0.397$.
Now we can work out $\theta$: $\tan\theta=\frac{1-t}{s}\approx 0.760$, so $\theta\approx 37.2^{\circ}$.
From the sine rule, we have $\frac{u}{\sin 30^{\circ}}=\frac{1}{\sin(150-\theta)}$, so $u=\frac{1}{2\sin(150-\theta)}\approx 0.542$.
Also from the sine rule, $n=\frac{\sin\theta}{\sin(150-\theta)}\approx 0.656$.
By looking at the longest line across the square, we have $\frac{1}{m+u+v}=\cos\theta$, so $v=\frac{1}{\cos\theta}-m-u\approx 0.317$.
By looking at the rectangle and considering the diagonal, we see that $(r+n)^2=(1+s)^2+t^2$, so $r=\sqrt{(1+s)^2+t^2}-n\approx 0.864$.
