Square world
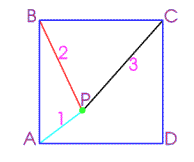
P is a point inside a square ABCD such that PA= 1, PB = 2 and PC =
3. How big is angle APB ?
Age
16 to 18
Challenge level
Problem
| $P$ is a point inside a square $ABCD$ such that $PA= 1$, $PB = 2$ and $PC = 3$. How big is ${\angle APB} $ ? |
Image
|
Getting Started
Pythagoras' theorem plays a part and you might like to rotate the square through $90$ degrees about $B$.
Student Solutions
Image
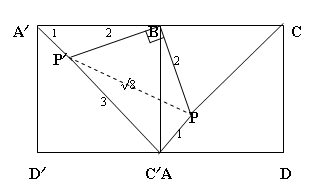
This beautifully neat solution was sent in by Johnny Chen.
If we rotate the figure by $90$ degrees about $B$ (clockwise).
This should result in a new square $A'BC'D'$ with a point $P'$
inside the new square such that, $\angle PBP'=90^{\circ}$ and
$BP=BP'=2$. By Pythagoras, $PP'= \sqrt 8$. Now consider triangle
$AP'P$. The side lengths are $3$, $\sqrt 8$, and $1$ which
satisfies Pythagoras again: $3^2 - 1^2 = (\sqrt 8)^2$.
So this triangle has $90$ degrees at $\angle P'PA$. Since we
know that $\angle BPP'=45^{\circ}$ therefore $\angle BPA$ is $135$
degrees.
This alternative method comes from Yatir from Maccabim-Reut High School, Israel.
Image
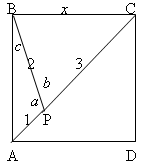
$AB=BC=CD=AD=x$, $BP=2$, $CP=3$, $AP=1$. Name the angles this way: $\angle ABP = c$, $\angle CBP = 90-c$, $\angle APB = a$, $\angle CPB = b$.
We need to find angle $a$. By the Sine Law:
and
Hence $\sin c = \sin a /x$, $\cos c = 3\sin b /x$ and we use the identity $\sin ^2 c + \cos ^2 c = 1$ to eliminate $c$. So
Using the Cosine Law we find $\cos b$ and then eliminate $b$:
Using the identity $\sin^2 b + \cos^2 b = 1$ we get
Finally we eliminate $x$. By the Cosine Law $x^2 = 4 + 1 - 4\cos a$ so
Combine (1) and (2) and simplify and we get:
This yields solutions: $a=45$ or $a=135$ degrees.
Now this angle cannot be $45$ degrees because angle $c$ is smaller ($AP$ is the shortest side of triangle $APB$) and the third angle of the triangle is less than $90$ degrees. Hence angle $a$ is $135$ degrees.