Fitting In
Problem
The largest square which fits into a circle is $ABCD$ and $EFGH$ is a square with $E$ and $F$ on the line $AB$ and $G$ and $H$ on the circumference of the circle. Show that $AB = 5EF$.
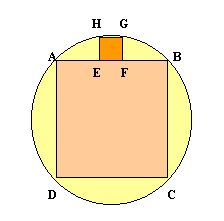
Similarly the largest equilateral triangle which fits into a circle is $LMN$ and $PQR$ is an equilateral triangle with $P$ and $Q$ on the line $LM$ and $R$ on the circumference of the circle. Show that $LM = 3PQ$.
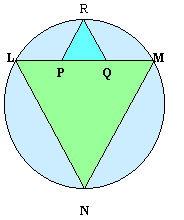
Student Solutions
Well done Freddie Manners (Packwood Haugh School) for this solution of the first part of the problem. Perhaps someone else can solve the second part.
If the radius of the circle is $r$, the length of each side of the square $r\sqrt{2}$ (Pythagoras' theorem).
Take a triangle from centre of circle to mid-point $HG$, mid-point $HG$ to $G$, and $G$ to centre. This is a right-angled triangle.
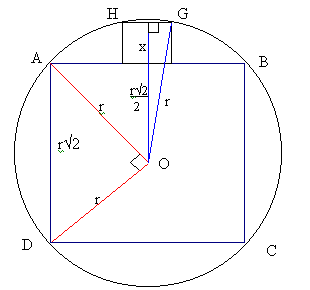
If the length of the sides of the small square is $x$, the sides of this triangle are:
$x/2$, $x + r\sqrt{2}/2$ and $r$.
By pythagoras, \[{({1\over 2}x)^2} + {( {r\sqrt2\over2} + {x})^2} = {r^2} \] \[{x^2\over4} + {2r^2\over4} + {xr\sqrt2} + {x^2} = {r^2} \] \[{x^2} + {2r^2} + {4xr\sqrt2} + {4x^2} = {4r^2} \] \[{5x^2} + {4xr\sqrt2} = {2r^2} \] Substitute $y = r\sqrt{2}$ (length of the side of the large square)
\[{5x^2} + {4xy} = {y^2} \] \[{5x^2} + {4xy} - {y^2} ={ 0} \] \[{x} = {{-4y \pm\sqrt{{(4y)^2} + {20y^2}}}\over 10} \] \[ {x} = {{-4y \pm\sqrt{36y^2}} \over 10} \] \[{x} = {{-4y \pm 6y}\over 10} \] \[ {10x} = {2y or -10y} \]
Ratio must be positive, therefore $10x = 2y$, therefore $y =
5x$
QED
Solution to part B.
Submitted by Samantha Gooneratne, Colombo International School, Sri Lanka. Well done Samantha! Her teacher also solved the problem using similar triangles, which I have include below Samantha's solution.
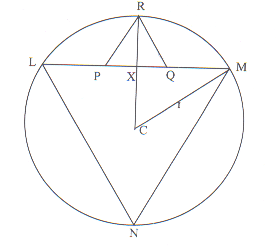
Let $X$ be the mid point of $PQ$, $C$ the center of the circle and $r$ the radius.
| $RX + XC = r$ Hence $PR \sin 60^{\circ}+ CM \cos 60^{\circ}=r$ \[{{\sqrt{3}\over 2}+ {{1 \over2}r} = {r}} \] Therefore \[{ {\sqrt{3}.PQ = {r}}} \] Now \[{{LM} ={2(r \sin 60)}} \] so
\[{{LM} ={\sqrt{3}.r}} \] \[{{LM} = {\sqrt{3}.(\sqrt{3}.PQ)}}
\] \[{{LM} = {3PQ}} \]
|
Image
|
Solution using similar triangles:
$NR$ is a diameter so $NLR = 90^{\circ}$
but $NLM = 60^{\circ}$ so $RLP = 30^{\circ}$
Now $LPR = 120^{\circ}$ so $LRP = 30^{\circ}$
Hence $LP = PR$ but $PR = PQ$
so $LP = PQ = QM$
$LM = 3 PQ$
