Sangaku
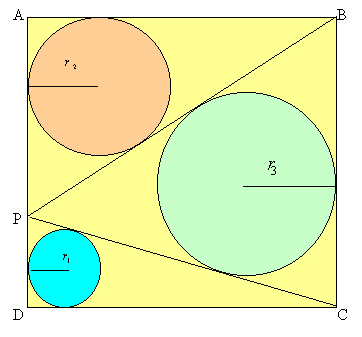
The square ABCD is split into three triangles by the lines BP and
CP. Find the radii of the three inscribed circles to these
triangles as P moves on AD.
Problem
The square $ABCD$ has sides of length 1 unit and it is split into three triangles by the lines $BP$ and $CP$. If $P$ is the midpoint of $AD$, find the radii of the inscribed circles of these triangles.
Now suppose the lengths $AP$ and $PD$ are $(1- p)$ and $p$ respectively. Find the radii of the three circles $r_1$, $r_2$and $r_3$ in terms of $p$ and plot, on the same axes, the graphs of $r_1$, $r_2$ and $r_3$ as $p$ varies from 0 to 1. Can the ratio of the radii $r_1 : r_2 : r_3$ ever take the value $1:2:3$?
Image
Notes and Background
Sangaku in Japanese means a mathematics tablet. During the Edo period (1603-1867) when Japan was cut off from the western world, people of all classes produced theorems in Euclidean geometry as beautifully coloured drawings on wooden tablets to be hung in a temple. Proofs were rarely given. The tablets challenged other geometers: "See if you can prove this."
Sangaku in Japanese means a mathematics tablet. During the Edo period (1603-1867) when Japan was cut off from the western world, people of all classes produced theorems in Euclidean geometry as beautifully coloured drawings on wooden tablets to be hung in a temple. Proofs were rarely given. The tablets challenged other geometers: "See if you can prove this."
Student Solutions
This solution is from Etienne of Parramatta Highschool, NSW Australia
I need to prove the area of a triangle $ XYZ $ is given by $ Area = rs $ where $ r $ is the radius of the incircle (inscribed circle) and $ s$ is the semi-perimeter (half the perimeter $ (x+y+z)/2$). Let $ x $, $ y $, $ z $ be the lengths of the sides of triangle $ XYZ $. Join the incentre $I$ of the triangle to the $3$ corners. From $I$ drop $3$ perpendiculars to each of the sides, each of these has a length of $ r $. The areas of $ XYI $, $ YZI $, $ ZXI $ are $ zr/2 $, $ xr/2 $ and $ yr/2 $ respectively. They sum up to give the area of triangle $ XYZ $
Area of $ XYZ = zr/2 + xr/2 + yr/2 = r(x+y+z)/2 = rs $.
Back to the question!
When $ P $ is the midpoint of $ AD, r_1 = r_2 $ because they sit on congruent triangles. The area of triangle $ ABP = AP \times AB/2 = 1/4. $
By Pythagoras' Theorem, $ PB = \sqrt(1+1/4) = \sqrt5/2. $
The semi perimeter of $ ABP = (1 + 1/2 + \sqrt5/2)/2 = [3+\sqrt5]/4. $ Using the formula $ A = rs $ for the area of the triangle, the area of $ ABP = r_1[3+\sqrt5]/4 = 1/4. $ This gives $ r_1 = 1/[3 + \sqrt5] = [3 - \sqrt5]/4 $ so $ r_1 = r_2 = [3 - \sqrt5]/4. $
The area of $BPC$ is $1 - 1/4 - 1/4 = 1/2$ and $ PB = PC = \sqrt5/2. $
The semi-perimeter of $ BPC = [1+ \sqrt5/2 + \sqrt5/2]/2 = [1 + \sqrt5]/2. $ From the area of triangle $ BPC $ we get $ r_3[1 + \sqrt5]/2 = 1/2 $ so $ r_3 = 1/[1 + \sqrt5] = [\sqrt5 - 1]/4. $
Now suppose the lengths AP and PD are $ 1-p $ and $ p $. The area of $ APB = (1-p)/2. $ The length $ PB = \sqrt(1 + p^2 - 2p + 1) = \sqrt(p^2 - 2p + 2) $ and the semi perimeter of $ APB = [1 + (1-p) + \sqrt(p^2 - 2p + 2)]/2.$ So, using the area formula again,
$$ r_2 = {1-p\over 2} \times {2\over [2 - p + \sqrt(p^2 - 2p + 2)]} = {1\over 2}[2 - p - \sqrt(p^2 - 2p + 2)]. $$
Similary with $ DPC $. The area of $ DPC = p/2 $ and the length $ PC = \sqrt(p^2 + 1). $ The semi perimeter of $ PC = [1 + p + \sqrt(p^2 + 1)]/2. $ So
$$ r_1 = {p\over 2} \times {2\over [1 + p + \sqrt(p^2 + 1)]} = {1\over 2}[1 + p - \sqrt(p^2 + 1)]. $$
Similarly $$ r_3 = {1\over 2} \times {2\over [1 + \sqrt(p^2 + 1) + \sqrt(p^2 -2p + 2)]} = {1\over 2}[1 + \sqrt(p^2 + 1) - \sqrt(p^2 -2p +2)][\sqrt(p^2 +1)- p]. $$
To finish this question you need to use the formulae found above which give the radii $ r_1 $, $ r_2$ and $ r_3 $ in terms of $ p $ and then consider how these values change as $ p $ varies from $0$ to $1$. For example $ r_1 $ varies from $0$ to approximately $0.293$ as $ p $ increases from $0$ to $1$.
Image
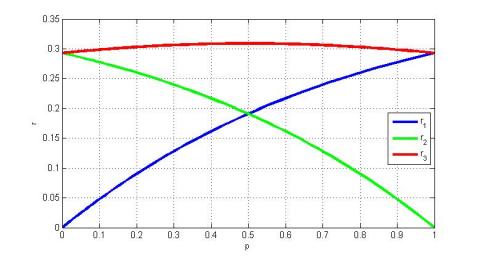
In order to discover whether the ratio of the radii $ r_1 : r_2 : r_3 $ can ever take the value $1 : 2 : 3$ you could look at the above graphs of $ r_1 $, $ r_2 $ and $ r_3 $ as $ p $ varies from $0$ to $1$.
$r_2$ must be twice the value of $r_1$ and by inspection you can see that the only place where this is possible is when $p$ is between $0.2$ and $0.3$. We also need $r_3$ to be $3/2$ times the value of $r_2$, but this is not the case when $p$ is between $0.2$ and $0.3$. Therefore the ratio $1:2:3$ can never occur.
