Circumspection
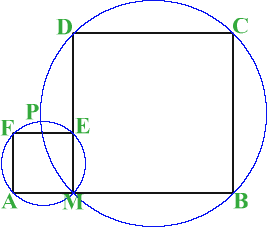
M is any point on the line AB. Squares of side length AM and MB are
constructed and their circumcircles intersect at P (and M). Prove
that the lines AD and BE produced pass through P.
Age
14 to 16
Challenge level
Problem
M is any point on the line AB. Squares of side length AM and MB are constructed and their circumcircles intersect at P (and M).
Prove that the lines AD and BE produced pass through P.
Image
Getting Started
Look for angles which will help you to show that the angles in question are $180^{\circ}$ so the lines are straight.
Student Solutions
M is any point on the line AB. Squares of side length AM and MB are constructed and their circumcircles intersect at P (and M).
Pick up a pencil, do some drawing, play with this. Look at angles APM, MPD, AEM, MCD and look for cyclic quadrilaterals. The proof that the lines AD and BE produced pass through P takes three or four lines.