Triangle Incircle Iteration
Problem
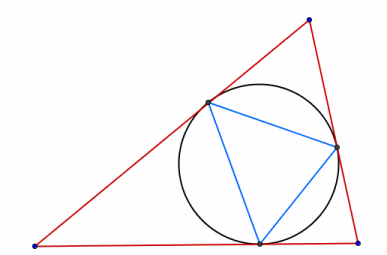
Start with any triangle. Draw its inscribed circle (the circle which just touches each side of the triangle). Draw the triangle which has its vertices at the points of contact between your original triangle and its incircle. Now keep repeating this process starting with the new triangle to form a sequence of nested triangles and circles. What happens to the triangles?
If the angles in the first triangle are $a$, $b$ and $c$ prove that the angles in the second triangle are given (in degrees) by
$f(x) = (90 - x/2)$
where $x$ takes the values $a$, $b$ and $c$. Choose some triangles, investigate this iteration numerically and try to give reasons for what happens.
Investigate what happens if you reverse this process (triangle to circumcircle to triangle...)
Getting Started
Have you noticed that, whatever triangle you start with, the nested triangles get more and more like equilateral triangles? In fact this convergence is very rapid.
The question tells you how to show why this happens by considering iterative sequences.
Student Solutions
Meg offers this solution:
The tangent of a circle is at right-angles to the radius of the circle. That is, if you join the centre point of the circle to a point where the circle meets the outer triangle, it makes an angle of $ 90 ^{\circ} $ with the side of the triangle.
The bisector of the angles of triangle $ABC$ will all pass through the centre of the circle.
From this we know that
$OAZ = \frac {a}{2}$ and $OZA = 90 ^{\circ}$
Hence $AOZ = 90- \frac{a}{2}$
Now consider triangle XOZ. This triangle is isosceles, so $OXZ = XZO = \frac{180-(180-a)}{2} = \frac{a}{2}$
By similar arguments
$OXY = OYZ = \frac{b}{2}$ and $OYZ = OZY = \frac{c}{2}$ Hence the new angles of the triangle are
$ZXY= \frac{a}{2}+\frac{b}{2}$
$XYZ = \frac{b}{2} + \frac{c}{2}$
$YZX =\frac{c}{2} + \frac{a}{2} $
$a+b+c=180 $
Hence $ \frac{a+b}{2}= 90 - \frac{c}{2}$
It follows that $ZXY =90 - \frac {c}{2}$.
A similar argument can be followed for $XYZ$ and $YZX$. If you continue drawing triangles within circles, the angles will decrease as shown here:
Triangle 1: a
Triangle 2: $ 90 - \frac{a}{2}$
Triangle 3: $90- \frac{90-\frac{a}{2}}{2}$ =$90 - \frac{90}{2} + \frac{a}{4}$
Triangle 4: $90- \frac{90-\frac{90}{2}+\frac{a}{4}}{2}= \frac{3}{4}.90 - \frac{a}{8}$
When you continue this iteration, you can demonstrate that the $a$ term becomes less and less significant, and the sum of the rest of the terms tends to 60 degrees. Hence the triangle tends to an equilateral triangle.
