Exploring Wild and Wonderful Number Patterns
Problem
Exploring Wild and Wonderful Number Patterns Created by Yourself!!
You've probably come across number patterns before; ones like :-
2 4 6 8 10 12 . . .
512 256 128 64 32 . . .
220 210 200 190 180 170 . . .
11 14 17 20 23 26 . . .
Work out the rules that produced each of the patterns.
What could be the reason for the series of dots appearing after each one?
Well, let's form some patterns of our own. But this time we will use two maths operations [for the maths person 'operations' mean adding, multiplying, dividing, subtracting etc.] to produce each new number in the pattern. You can probably multiply, add, subtract and divide. Because dividing sometimes can leave bits left over, let's ignore that one for the time being.
Adding put together with subtracting results in something that we could have got just by adding or subtracting. Let me show you:-
Suppose you decided that you would add 5 and subtract 2 each time . . . . then you might as well just be adding 3 each time.
OR suppose you decided to add 6 and subtract 11 each time . . . . then you might as well just be taking away 5 each time.
I therefore suggest that we make a rule about the two operations that we will use for this exploration.
RULE :- You will use multiplication with either adding or subtraction. BUT you can have the multiplication last if you like.
So let's get started, you will need to do 5 things for this work:
a) You need to choose a STARTING NUMBER (In my example suppose it's 7)
b) You need to decide which OPERATION to do first [addition, subtraction or multiplication] (In my example suppose it's multiplication )
c) You need to decide what NUMBER to use with the operation you chose in b (In my example suppose it's 3 )
d) You need to decide on your next OPERATION (I chose to use multiplication before so it's got to be addition or subtraction, suppose it's subtraction)
e) You need to decide what NUMBER to use with the operation you chose in d. (In my example suppose it's 3)
Let's run through this a bit.
Starting number 7 [ x 3 - 3 ] gives 18
Now we use 18..... [ x 3 - 3 ] gives 51
Now we use 51..... [ x 3 - 3 ] gives 150
I think it would be better to write it down without the brackets bit, although we do have to do both operations before we write the result down and it would be helpful to write it all out in columns going down:-
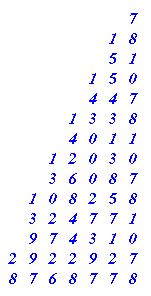
I now write down ALL THE THINGS THAT I NOTICE ABOUT THIS PATTERN.
Things like:-
The answers go odd, even, odd, even . . . . .
The units figures go 7 8 1 0 , 7 8 1 0 , . . . etc.
You might be able to see lots more, I've just written down a few quick ones.
When I've had a good long, hard look and talked with others, perhaps, I do the next stage; which is:-
Take a look at a, b, c, d, e, that I used and make a SMALL CHANGE
SUPPOSE I decide to change e, to subtracting 4 instead of 3 BUT everything else stays the same so:-
Starting Number 7 [ x 3 - 4 ] gives ......
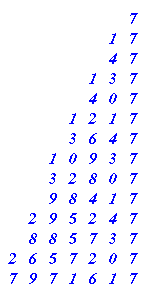
Like before I write down all the things that I notice :-
LIKE :-
The answers all end in a 7
The tens figures go 4 3 0 1, 4 3 0 1 . . .
AND maybe many more things.
Then I COMPARE what I noticed this time with last time, similar things and rather different things.
SO I might write something like:-
In the first pattern the units went in a pattern of 4 repeating different figures, in the second pattern it's the tens that do that. Both patterns end with a 7 every 4th one. I also notice that in the units of the first you could say that the 8 - 1 gives 7!
WELL after that L O N G introduction it's time for you to have a go!
1) Choose you five things to start off with a, b, c, d, e.
2) Produce at least 8 answers underneath each other in good columns [it helps to see tens patterns etc.].
3) Write about the things you notice.
4) Make one small change in the 5 starting things a, b, c, d, e.
5) Do 2) and 3) again.
6) Compare what's happened this time with the first time.
Student Solutions
Saul did this using 6 - 3 x 8;
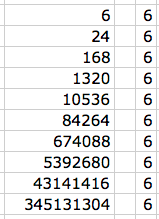
Emma did 2, firstly 9 x 3 + 1, then 10 x 2 - 3;
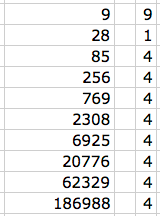
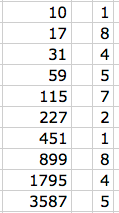
Jennifer did this by using 6 x 4 - 4;
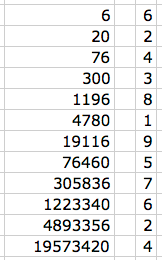
Sophie did this using 4 x 3 + 8;
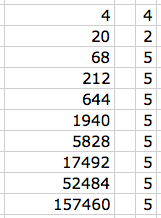
Mariko used 9 x 3 + 9;
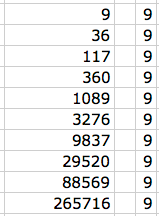
Tom explored 4 x 9 - 13
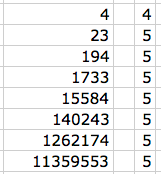
Sara looked at 3 x 5 - 2
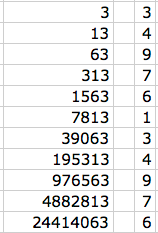
Stephanie used 4 x 7 - 10

she noticed that the units doubled from 4 to 8 to 6 to 2 then go back to 4
Thank you St. Lukes for this really good work, well done and keep on with your work sending in your solutions to the live problems.
One pupil from another school (don't know which) explored a great deal and here we summarize what was found :-
RULE UNITS DIG.ROOTS OTHER COMMENTS
3 x 8 + 4 8.... 1 3 1 3 1 3 ... Tens > 2 Hunds > 2860....
4 x 8 + 4 6204 ... 9 4 9 4 9 4 ...
5 x 8 + 4 4260 ... 8 5 8 5 8 5 ...
6 x 8 + 4 2046 ... 7 6 7 6 7 6 ...
7 x 8 + 4 0462 ... 6 7 6 7 6 7 ...
8 x 8 + 4 8... 5 8 5 8 5 8 ... Tens > 6480
9 x 8 + 4 6204 ... 4 9 4 9 4 9 ...
10 x 8 + 4 4620 ... 3 1 3 1 3 1 ... So we could predict that the next ones go:-
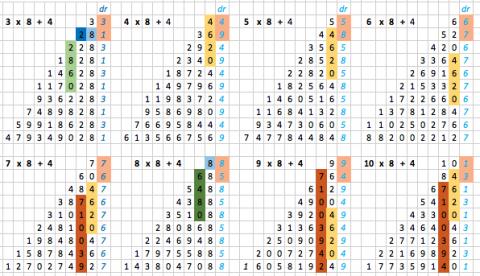
11 x 8 + 4 2 ... 2 ... Dig. Roots should be 2, 11 but 11 is 2 so all are 2!
12 x 8 + 4 0462 ... 1 3 1 3 1 3 ...
13 x 8 + 4 8 ... 9 4 9 4 9 4 ... Checked, and Tens > 0648....
Well reading this has been very exciting and led Bernard to make a further change, using 7 instead of 8.
RULE UNITS DIG.ROOTS OTHER COMMENTS
2 x 7 + 4 8024... 945378612 .. Tens > 1310 ...
3 x 7 + 4 5973... 786129453 .. Tens > 2750 ...
4 x 7 + 4 2804... 537861294 .. Tens > 3200 ... Hunds > All even
5 x 7 + 4 9735... 378612945 .. Tens > 3740 ...
6 x 7 + 4 6... 129453786 .. Tens > 4280 ... Hunds > 3200...
7 x 7 + 4 3597... 861294537 .. Tens > 5720 ...
8 x 7 + 4 0428... 612945378 .. Tens > 6270 ...
9 x 7 + 4 7359... 453786129 .. Tens > 6710 ...
10 x 7 + 4 4280... 294537861 .. Tens > 7251 ...
11 x 7 + 4 1... 945378612 .. Tens > 8701 ... Hunds > 5000 Thous > Even
Teachers' Resources
Why do this problem?
This activity, I have found to be very enjoyable for pupils, because it opens up a new world for most of them - that they can create their own number patterns and explore them! It's a healthy change for many of them to feel that they are not just being handed something that the teacher already knows an awful lot about. So if these thoughts encourage you then present it to your pupils.
Possible approach
Key questions
Possible extension
Possible support
Extra
The patterns that are generated can be very exciting. I find it useful if the children have already met things like the patterns that are evident in the nine times table to take things a bit further and investigate Digital Roots. I have also found that following the a, b, c, d, e parts as suggested in this activity, writing what they notice, changing something slightly and repeating etc. to be a very good investigational process for the youngsters to get used to. Caleb Gattegno in the 1960s said; "Mathematics is the study of the invariances under a set of transformation". Or if you prefer it, in my words now; "Doing mathematics is taking something, changing it in some way and observing what is the same and what is different."
