Picture Story
Can you see how this picture illustrates the formula for the sum of the first six cube numbers?
Problem
Picture Story printable worksheet
Take a look at the video below.
Can you describe what happens?
Can you explain how the video might continue, if more little cubes were available?
Can you be sure that the patterns in the video will carry on?
Can you use algebra to represent the patterns you saw?
Getting Started
The picture below shows how the slices of cube were arranged in the video.
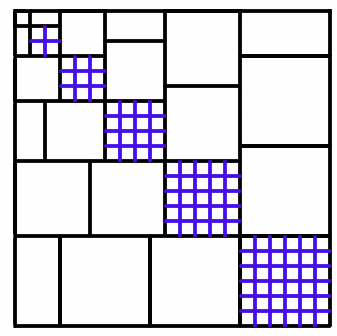
Student Solutions
Jack and Ashley from Sir Harry Smith Community College sent us the following thoughts:
$(1+2+3+...+n)^2$ is equal to $1^3+2^3+3^3+...+n^3$, which can also be written $$\left(\sum_{r=1}^n r \right)^2 = \sum_{r=1}^n r^3$$
We tested this formula with two examples:
$1^3+2^3+...+6^3=441$, and $1+2+...+6=21, 21^2=441$.
$1^3+2^3+...+10^3=3025$, and $1+2+...+10=55, 55^2=3025$.
An anonymous solver from Mearns Castle School explained very clearly how the diagram shows the two parts of the formula:
The area of the square can be looked at in different ways.
The columns are $1$ then $2$ then $3$ then $4$ units long. It is a square, so the area is the length squared which is $(1+2+3+4+5+6)^2$.
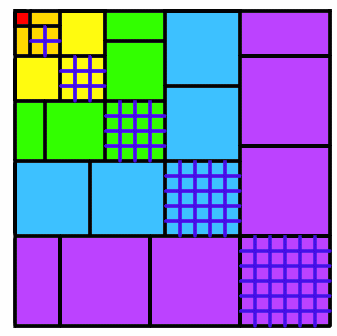
Now look at each of the 6 backward L shapes.
We have the indicated square on the diagonal (for example, on the blue L shape $5^2$), then we have other congruent squares (shaded in the same colour).
Note that in even levels, there are two half-squares which make up one full square. So the area of the blue shaded level is: $5^2+4\times5^2 = (5^2)(1+4) =(5^2)(5) =5^3$
As this is true for the first, second, third... $n^{th}$ level of the area of the $n^{th}$ level is $n^3$.
This means if there are $n$ levels, the length of one side of the square is $1+2+3...+(n-1)+n$ and thus the area equals $(1+2+3...+(n-1)+n)^2$.
But considering the area in terms of each level gives $(1^3)+(2^3)+(3^3)...+(n-1)^3+(n^3)$.
So it can be said $(1^3)+(2^3)+(3^3)...+(n-1)^3+(n^3) = (1+2+3...+(n-1)+n)^2$.
John from Takapuna Grammar School used induction to prove the formula:
Using induction we should first prove that $1^3$ is equal to $1^2$, which is obvious, as they're both equal to $1$.
Now to prove that any added number $(n+1)$ would keep the equation satisfied:
The formula for any triangular number $(1 + 2 + 3...+ n)$ is $\frac{n(n+1)}{2}$.
Now we observe the way in which new tiles are put on. There are $(n+1)$ squares to be added, which contain $(n+1)^2$ units each, making $(n+1)^3$.
One of these squares is placed diagonally to the original square and the other $n$ squares are placed along the sides.
Since there are two sides to place against, this means that there are $\frac{n}{2}$ squares per side, and because each square is $(n+1)$ units long that means there are $\frac{n(n+1)}{2}$ units covered on each side.
There are $\frac{n(n+1)}{2}$ units on each side of the original square so that means all of the units on each side are covered, leaving the last $(n+1)^2$ square (the one that is diagonal to the original square) to make a new square itself.
Finally, we know that each side of this new square is the $(n+1)^{th}$ triangular number, because the previous square's length was the $n^{th}$ triangular number, and this length has increased by (n+1).
Therefore the equation $(1^3 + 2^3...n^3)=(1 + 2... + n)^2$ holds for all positive whole numbers, because it is true for n=1 and if it's true for any number n then it's true for n + 1.
Teachers' Resources
Why do this problem?
This problem encourages visualisation of a three dimensional idea in a two dimensional context. It offers a visual demonstration of the sum of cubes which can lead to a proof. By extending the picture, ideas of proof by induction could be introduced.
Possible approach
This printable worksheet may be useful: Picture Story.
Perhaps start by exploring the problem Picturing Triangle Numbers, which develops the formula for the nth triangular number using a pictorial approach.
Are they surprised by the patterns they have noticed?
Can they draw similar images or extend the existing image to represent the sum of the first 7, 8, 9, 10 cubes? Does this support their predictions above?
Can they now deduce the general formula for the sum of the first n cube numbers? In small groups, they could develop pictures to support a proof of their generalisation, which could be presented to the rest of the class.
Key questions
Where are the cube numbers in the picture?
How does the picture show $(1+2+3+4+5+6)^2$?
Could you draw similar pictures for other sums of cubes? Can you always draw such a picture?
Possible support
Try the problems Picturing Triangle Numbers and Picturing Square Numbers.
Possible extension
The problem Summing Squares offers a similar visual proof idea in three dimensions for the sum of the first n square numbers. Students could read the article Proof by Induction to find out more about this important method of proof.
