Plane to see
P is the midpoint of an edge of a cube and Q divides another edge
in the ratio 1 to 4. Find the ratio of the volumes of the two
pieces of the cube cut by a plane through PQ and a vertex.
Age
16 to 18
Challenge level
Problem
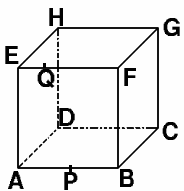
In the cube illustrated the point $P$ is the midpoint of $AB$ and the point $Q$ is one quarter of the way along the edge $EF$.
The plane through $PDQ$ cuts the cube into two. Find the ratio of the volumes of the two pieces.
Image
Getting Started
Where does the plane $PDQ$ meet the line $EH$?
Imagine a vertical line through $A$. Where does the plane $PDQ$ meet this line?
The method only needs similar triangles and similar 3D shapes.
It is not necessary, but it may help, to use coordinates with the origin at $A$.
Student Solutions
The problem can be solved, without using 3D coordinates, by essentially the same argument as the one used in the solution below. You have to locate the same points, and use similar triangles and the volumes of similar tetrahedra.
This solution came from Brad of Kokomo School, India and a very similar solution fromSue Liu of Madras College, St Andrews.
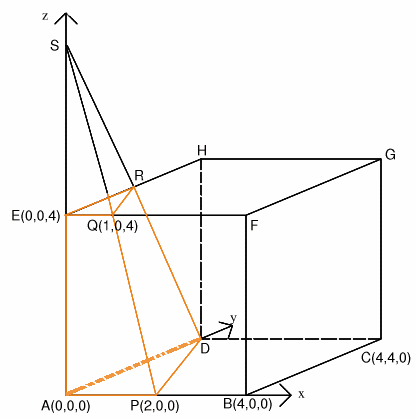
Using 3D coordinates with point $A$ at the origin, $B$ being the point $(4, 0, 0)$, $C$ the point $(4, 4, 0)$, $D$ the point $(0, 4, 0)$, $E$ the point $(0, 0, 4)$ etc as shown in the diagram. The point $P$ which is the midpoint of $AB$ has coordinates $(2, 0, 0)$ and $Q$, which is a quarter of the way along $EF$ has coordinates $(1, 0, 4)$.
Image
The general equation of a plane is $ax + by + cz = 1$ and to find $a$, $b$ and $c$ we only need to know three points in the plane. Hence it is easy to find the equation of the plane through $D$, $P$ and $Q$. Substituting the coordinates of the points into the equation of the plane we get:
$ 4b = 1 $
$ 2a = 1 $
$ a + 4c = 1 $
This gives $a = 1/2$, $b = 1/4$ and $c = 1/8$. Writing the equation of the plane without fractions we get
Now $RE = 2$, $EQ = 1$, $\angle \rm{ REQ} = 90^\circ$, and DA = 4, AP = 2, $\angle \rm{ DAP} = 90^\circ$ so it follows that the triangles $REQ$ and $DAP$, which lie in parallel planes, are similar. Also, if we extend the lines $AE$, $PQ$ and $DR$ they will meet at one point $S$ where $SE = 4$ and $SA = 8$.
The points $S$, $A$, $P$ and $D$ are the vertices of a tetrahedron which is sliced into two parts by the plane through $R$, $E$ and $Q$. The required volume of the section of the cube is given by subtracting the volume of the tetrahedron $SEQR$ from the volume of the tetrahedron $SAPD$.
Volume of smaller section of cube
$ = {1\over 3}(32 - 4) = {28\over 3}. $
The volume of the whole cube is $64$ cubic units so the ratio of the volume of the smaller piece to the volume of the cube is $7$ to $48$. The ratio of the volumes of the two pieces of the cube is $7$ to $41$.
Teachers' Resources
Why do this problem?
It provides good eperience of visualisation in 3D and using ideas of similarity and scaling in 2D and 3D. They will need the formula for the volume of a tetrahedron.
It is not necesary to use 3D coordinates but they can be useful.
Possible approach
Emphasise the value of trying to visualise the plane cutting the cube. Suggesthe students close there eyes and try to visualise where the plane cuts the vertical line through $A$.
Suggest students look for similar triangles and similar 3D shapes.
Key question
Where does the line $EH$ cut the plane $PDQ$? Call this point $R$.
Where do the lines $PQ$ and $DR$ meet?