Napoleon's Hat
Three equilateral triangles ABC, AYX and XZB are drawn with the point X a moveable point on AB. The points P, Q and R are the centres of the three triangles. What can you say about triangle PQR?
Problem
Image
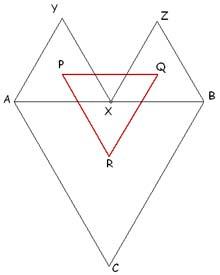
| The diagram shows three equilateral triangles $ABC, AYX$ and $XZB$. The point $X$ is a moveable point on $AB$. The points $P$, $Q$ and $R$ are the centres of the three triangles.
Experiment with the dynamic diagram.
What can you say about triangle $PQR$?
Can you prove your conjecture? |
Created with GeoGebra |
You can download your own free copy of Geogebra from the above link and draw your own dynamic diagrams.
Getting Started
One possibility is to use coordinates. You need to use the coordinatesof the centroids of the triangles.
Student Solutions
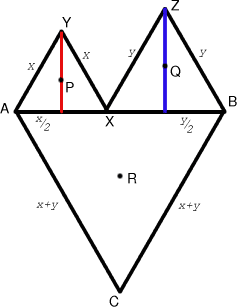
This is Sue Liu's solution proving that the triangle $PQR$ is equilateral whatever the position of the point $X$. Many congratulations Sue on all your excellent work.
Let $AX = x$ and $XB = y$ where we know that $AX + XB = AB$ (constant). Let the points $P, Q$ and $R$ be the centres (centroids) of the triangles $\Delta AXY, \Delta XZB$ and $\Delta ABC$ respectively. We use the fact that the medians of a triangle intersect at the centroid and this point divides the medians in the ratio one third to two thirds. If we set the point $A$ as the origin, then the points $P$, $Q$ and $R$, being the centroids of the equilateral triangles $AXY$, $XZB$ and $ABC$, have coordinates
$P = ({1\over 2}x, {\sqrt 3\over 6}x),$
$Q = (x + {1\over 2}y, {\sqrt 3\over 6}y)$, and
$R = ({1\over 2}(x + y), {-\sqrt 3\over 6}(x +y)).$
We now show that the lengths $PQ$, $QR$ and $RP$ are equal. $$\eqalign{ PQ^2 &= (x + {1\over 2}y - {1\over 2}x)^2 + ({\sqrt 3\over 6}y - {\sqrt 3\over 6}x)^2 \cr &= {x^2 + 2xy + y^2\over 4} + {y^2 - 2xy + x^2 \over 12} \cr &= {x^2 +xy +y^2 \over 3}.}$$ $$\eqalign { QR^2 &= ({1\over 2}(x + y) - (x + {1\over 2}y)^2 + (-{\sqrt 3\over 6}(x + y) - {\sqrt 3\over 6}y)^2 \cr &= {1\over 4}x^2 + {1\over 12}(x^2 + 4xy + 4y^2) \cr &= {x^2 +xy +y^2 \over 3}.}$$ $$\eqalign { RP^2 &= ({1\over 2}(x + y) - {1\over 2}x)^2 + (-{\sqrt3 \over 6}(x + y) - {\sqrt 3\over 6}x)^2 \cr &= {1\over 4}y^2 + {1\over 12}(4x^2 + 4xy + y^2) \cr &= {x^2 +xy +y^2 \over 3}.}$$ As $$PQ = QR = RP = \sqrt {{x^2 + xy + y^2 \over 3}}$$ for any $x$ it follows that $\Delta PQR$ is equilateral whatever the position of $X$.
Teachers' Resources
Why do this problem?
Learners can investigate using the interactivity, make a conjecture and then try to prove their own conjecture.
It can be an exercise in coordinates.
It is useful for learners to appreciate that the symmetry of the result makes it unnecessary to work out all three distances.
Possible approach
Ideally learners would work independently on this problem.
Key question
How do we find the coordinates of the centroid of an equilateral triangle?
Possible support
GeoGebra is FREE educational mathematics software and your learners can experiment with it and draw their own dynamic diagrams.
