Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
Problem
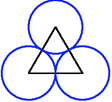

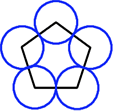
For any regular polygon it is always possible to draw circles with centres at the vertices of the polygon, and radii equal to half the length of the edges, to form a "polycircle" in which each circle just touches its neighbours.
Investigate and explain what happens in the case of non-regular polygons. Is it always possible to construct three circles with centres at the vertices of the triangle so that the circles just touch?
Try a numerical example, say the 3 points give a triangle of sides 12, 15 and 13. Find the radii of the circles.
Now use the same method when the sides of the triangle are $a$, $b$ and $c$.
Generalise still more! What about 4 circles around a quadrilateral? 5 circles around a pentagon? $n$ circles around an n-gon?
You may wish to use GeoGebra to explore.
Getting Started
Try a numerical example, say the 3 points give a triangle of sides 12, 15 and 13. Find the radii of the circles.
Now use the same method if the sides of the triangle are $a$, $b$ and $c$?
Generalise still more: What about 4 circles? 5 circles? $n$ circles?
Student Solutions
Four people cracked this one: Bella and Andaleeb from Woodhouse Sixth Form College, Sue from Madras College and Alexander from Shevah-Mofet School.
Bella started her answer by trial and error for different triangles
For the triangle of side c = 15, b = 13, a = 12:
I split the longest side (c = 15) into7 and 8, and draw 2 circles: (A, 8), that is circle with center A and radius8, and (B, 7). These 2 circles cut the 2 sides at P and Q.So CP = 13 - 8 =5 and CQ = 12 - 7 = 5. So I drew the cirle(C, 5), which just touches the other 2 cirles
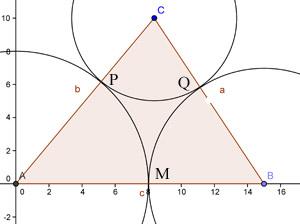
From the result above, I realize important rules to tackle the problem:
First, the difference between the 2 radii on 1 side of the triangle is equal to the difference of the 2 other sides. More specifically, AP - PC = 8 - 5 = 3 and AB - CB = 15 - 12 = 3, which means AP - PC = AB - CB. Similarlly, BQ - CQ = BA - BC = 2 and AM - MB = AC - BC = 1.
Second, the larger radius is corresponding to the larger side. For example, AB > CB. When we split AC into AP and CP, AP will be greater than CP.
These rules imply that I can always find the radii simply by splitting 1 side of the triangle such that the difference between the 2 numbers equals the difference between the 2 other sides and the larger number is corresponding to the larger side of the triangle.
I tried it out for another triangle of different size and it worked perfectly. For the triangle of side c = 10, b = 8, a = 4:

Because AB - CB = 10 - 8 = 2. I split the remaining side AC such that AP - PQ = 2. There is only the pair (1,3) which satisfy that condition. So AP = 3 and CP = 1 since AB > CB. So 3 circles are (A, 3); (B, 7); and (C, 1).
I can also prove these rules.
Assume that we can draw 3 circles which statisfy the conditions as shown by the graph
Look at the 2 sides of the triangle AB and BC:
AB = AM + BM
BC = BQ + CQ
BM = BQ
So AB - BC = AM - CQ (1)
Look at the remaining side AC:
AP = AM and CP = CQ (2)
From (1) and (2) we have:
AB - BC = AP - CP
As long as AB > BC, AP will be greater than CP
In words, this implies the rules (Q.E.D.)
Alexander sent us a more general solution.
Suppose it is possible for the triangle with sides $12$, $13$ and $15$ and the radii of the circles are $r_1$, $r_2$, $r_3$. Then
$\begin{eqnarray} \\ r_1 + r_2 &=& 12\\ r_2 + r_3 &=& 13\\ r_3 + r_1 &=& 15. \end{eqnarray}$
This set of simultaneous equations is easily solved to give $r_1 = 7$, $r_2 = 5$ and $r_3 = 8$. So we have proved that polycircles exist for this triangle.
Let's prove that it's possible for any triangle to construct circles with centres at the vertices so that the circles just touch. Let $a$, $b$ and $c$ be the sides and $r_1$, $r_2$, $r_3$ the radii of the circles. The only constraints on the radii are: $r_1> 0$, $r_2> 0$, $r_3> 0$. \begin{eqnarray} \\ r_1 + r_2 &=& a \\ r_2 + r_3 &=& b \\ r_3 + r_1 &=& c. \end{eqnarray} The solution for this system is: \begin{eqnarray} \\ r_1 &=& \frac{(a + c - b)}{2} \\ r_2 &=& \frac{(a + b - c)}{2} \\ r_3 &=& \frac{(b + c - a)}{2} \end{eqnarray} and since the sum of the lengths of any 2 sides in a triangle is bigger than the 3rd side, there are solutions for any positive $a$, $b$ and $c$.
Now consider a convex polygon with $n$ sides: $a_1$, $a_2$, $a_3$,...$a_n$. Suppose circles can be drawn with centres at the vertices of the polygon such that the circles just touch each other. Let $r_1$, $r_2$, $r_3$,... be the radii. Then: \begin{eqnarray} \\ r_1 + r_2 &=& a_1 \\ r_2 + r_3 &=& a_2 \\ ... \\ r_n + r_1 &=& a_n. \end{eqnarray} Let's try to figure out what $r_1$ equals, and all the other solutions will of course be symmetrical. \begin{eqnarray} \\ r_1 &=& a_n - r_n = a_n - a_{n-1} + r_{n-1}\\ &=& a_n - a_{n-1} + a_{n-2} - r_{n-2} = ...\\ &=& a_n - a_{n-1} + a_{n-2} - ...+(-1)^{n-1}a_1 + (-1)^nr_1. \end{eqnarray} If $n$ is even then $r_1 = a_n - a_{n-1} + a_{n-2} - ... - a_1 + r_1$ which means that the condition for the existence of solutions is: $$a_n - a_{n-1} + a_{n-2} - ... - a_1 = 0.$$ It also means that if this condition holds there are an infinite number of solutions and if it does not hold there are no solutions.
If $n$ is odd then what we get is $$r_1 = \frac{1}{2}(a_n - a_{n-1} + a_{n-2} - ... + a_1)$$ and $r_1$ is positive when $(a_n - a_{n-1} + a_{n-2} - ... + a_1) > 0.$
For polygons with an odd number of sides solutions always exist but 'negative' values of $r_i$ occur when, instead of touching externally, one circle surrounds its 'neighbour' which touches it internally so the length of the edge is given by the difference of the radii and not the sum of the radii.
Teachers' Resources
Why do this problem?
This problem is accessible for different age groups. It is a rich problem that provides suitable challenges for a wide age range. Younger learners can find solutions for three circles given the sides of a triangles by trial and improvement.
Once the learners can solve two simultaneous linear equations in two unknowns then they can be challenged to solve this problem by solving three simultaneous equations. Because the coefficients are all unity the equations are easy to solve.
This problem is often used at stages 3 as well as 4. At Stage 5 it is useful as an application of solving simultaneous linear equations and the question about which polygons have solutions and which do not can take learners into linear algebra.
The problem demonstrates a powerful inter-relationship between geometry and algebra.
Possible approach
For younger learners who know how to solve a pair of simultaneous linear equations this problem provides a good series of challenges. Taking a numerical example where the lengths of the sides of the triangle are known (see the Hint), and the radii of the polycircles has to be found, then three simultaneous linear equations can easily be found and solved. Even though learners may only have been taught to solve two simultaneous equations in two unknowns many will be able to solve these three equations for themselves and get satisfaction from being able to do so independently. The results can be checked by drawing.
The next step is to generalise from a particular numerical example and to use exactly the same steps in the algebra to derive formulae for the radii in terms of the lengths of the sides of the triangle. This is a good exercise in a concrete setting for working with algebra.
Learners who have succeeded so far can explore the existence of polycircles for quadrilaterals and pentagons and how the algebra explains the different geometrical phenomena that arise.
For older learners who have been been introduced to linear algebra, the generalisation of the problem to polygons with n sides provides a challenge to explain why there are unique solutions for certain values of n and not for others.
Possible support
The problem is written to start with a numerical special case of a triangle in order to support younger and less confident learners. They may first try trial and improvement where the problem is like arithmagons. From that they may be able to develop a method for finding solutions in the general case and even for getting the formula without the use of simultaneous equations.
Possible extension
You could pose the problem for general polygons and leave the learners to decide for themselves whether or not to start with special cases.
