Property Chart
A game in which players take it in turns to try to draw quadrilaterals (or triangles) with particular properties. Is it possible to fill the game grid?
Problem
Property Chart printable sheet - grid and instructions
Property Chart printable sheet - quadrilateral cards
Property Chart printable sheet - triangle cards
Printable spotty paper - square grid, isometric grid
Shuffle eight of the quadrilateral cards, and lay them on the grid in the spaces marked "property card". Your challenge is to draw a quadrilateral in each square, so that the quadrilateral has both the properties at the top of the column and at the start of the row. There might be some that aren't possible! If you like, you could play this with a friend, taking turns to draw shapes. If you can't draw a shape, pass and see whether your partner can, the winner is the one who draws the last shape.
You might find it helpful to draw the shapes on spotty paper; there are squares here and isometric paper here (this might help you find areas and angles).
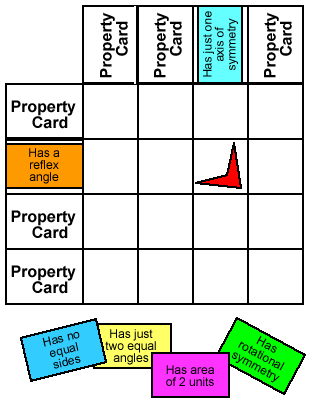
What's the smallest number of different shapes you need to fill in the grid? What shapes are these, and what cards did you use?
Getting Started
You'll have to use some experimentation here, to get a feel for what does and doesn't work.
Do you think you could fill the whole grid using just one shape, if you chose the right 8 cards? What sort of quadrilateral might have lots of nice properties?
It's pretty obvious that you can't come up with a shape that has just 1 axis of symmetry and more than 1 axis of symmetry, so if you put one of these at the start of a row and the other at a start of a column, you know that you won't be able to fill in the square where they intersect. Can you think of any other combinations like this? Is it possible to choose them so that you can't fill in any of the squares?
Student Solutions
Samantha from Hamlin sent us her work on this problem. She found that it is possible to choose cards so that all of the boxes can be filled in. In fact, she chose cards so that she could fill in all of the boxes using a 1x1 square! Here is her example :
| Has all equal angles | Has rotational symmetry | Has more than 1 axis of symmetry | Has area of 1 unit | |
| Has more than 2 equal angles | square | square | square | square |
| Has more than 1 right angle | square | square | square | square |
| Has more than 2 equal sides | square | square | square | square |
| Has 2 pairs of parallel sides | square | square | square | square |
Well done to Christine, Peter, Rebecca and Josh from Ely St John's School who found two more ways to choose cards so that all the boxes could be filled in. They decided to use rectangles as well as squares. Here is one of their solutions:
| Has more than 1 axis of symmetry | Has all equal angles | Has more than 2 equal angles | Has 2 pairs or parallel sides | |
| Has more than 1 right angle | square | square | square | square |
| Has more than 2 equal angles | square | square | square | square |
Has area of 1 unit | square | square | square | square |
Has area of 2 units | rectangle | rectangle | rectangle | rectangle |
George found that it is possible to choose cards so that none of the boxes can be filled in. Here's the example he sent us:
| More than one axis of symmetry | Just two pairs of parallel sides | Rotational symmetry | All angles equal | |
| Just one axis of symmetry | ||||
| Just one pair of parallel sides | ||||
| Just two equal angles | ||||
| One right angle |
If anyone has had a go at these questions using the triangle cards, do send your solutions to the secondary team.
Teachers' Resources
Why do this problem?
This game provides an interesting context in which to consider the properties of quadrilaterals (or triangles), and has a particular focus on the combinations of properties that are possible.
Possible approach
Quadrilaterals Game could be used either at the beginning or at the end of this problem.
Use the instructions on the problem page to set up and play the game in pairs. As you circulate, rather than praising the winner of each game, praise charts that are fuller when the game ends - or at least where you believe all of the possible shapes have been drawn. Once a game has been 'won', encourage the pair to work together to check if there were any spaces that could have been filled - or to convince each other that the remaining spaces cannot be filled.
Once students have had a chance to play and explore the game, bring the whole group together to share what they have noticed. Were there any cards which they found easy or difficult to draw shapes for? Which were the best and worst combinations of cards? Encourage a range of opinions, and where there is disagreement, challenge students to justify their ideas and convince each other.
Next, introduce the questions at the end of the problem. Students could work on them in their pairs, or in new groups of three or four. Remind them to use the ideas from the whole group discussion, and to use what each student learnt from playing the game. Groups could draw their final grids, and then look around the room at each others' grids. How many different complete grids can the whole group come up with?
Key questions
- Which shapes are most useful in this game?
- Which property cards are 'good' and 'bad' and why?
- Tell me two cards where there is no shape that works for both.
Possible support
The game could be played as a whole class - shuffle and arrange the property cards on the board so that everyone has the same question. Groups of 3 or 4 then work together filling in the grid and checking each others work. A correct shape or gap will earn 10 points, but each incorrect shape or gap will lose 10 points. After a set time, all the grids are displayed, and students try to find errors in the other groups' work, in order to establish the scores and the winners. They may be ready to try the problem as stated after this!
Possible extension
Suggest students have a go at Shapely Pairs
Additional comment
Teachers may be interested in Gillian Hatch's article Using Games in the Classroom in which she analyses what goes on when mathematical games are used as a pedagogic device.
