Giant Holly Leaf

Stage: 4 Challenge Level:

The following solution is based on the work of Ben and Sarah. Well done to both of you.

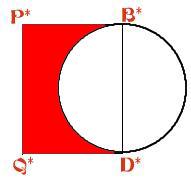
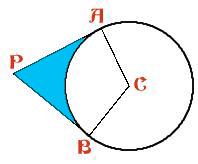
The boundary of the holly leaf can be divided into sections. There are two sections made up from arcs of a circle like the first diagram (above) and there are eight arcs like the second diagram above. So that boundary can be calculated by finding the sum of the lengths of these arcs

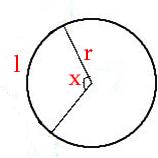
The length of an arc can be calculated by the following formula:
$l$ = $rx$ ($x$ measured in radian)

$\angle APB$= 360degrees - $\angle PAC$ - $\angle PBC$ - $\angle ACB$ = (360 - 90 - 90 - 125) degrees = 55 degrees

P*B*D*Q* is a rectangle, so $\angle Q$*$P$*$B$* = 90 degrees

180 degrees correspond to $\pi $, so 55 degrees can be converted into 55$\pi$/180 or 11$\pi$/36; and 90 degrees are equivalent to 90$\pi$/180 or $\pi$/2

So the length of the arc subtending the angle APB is: 11$\pi$r/36, and that subtending the angle B*P*Q* is $\pi$r/2

Hence the length of the boundary of the yellow area is:

4 $\times$ 11$\pi$r/36 + 2 $\times$ $\pi$r/2 = 20$\pi$r/9

The parameter of the holy leaf is formed by 8 arcs subtended by angle ACB and 2 semi-cirles .

If $\angle ACB$ = 125 degrees, the parameter of the holy leaf is:
8 $\times$ (5 $\times$125$\pi$/180) + 2 $\times$ 5 $\times$ $\pi$ = 340$\pi$/9 = 118.68 cm

If$\angle ACB$ = 135 degrees, the parameter of the holy leaf is:
8 $\times$ (5 $\times$ 135$\pi$/180) + 2 $\times$ 5 $\times$ $\pi$ = 40$\pi$ = 125.66 cm > 118.68cm

The area of the holy leaf is formed by 8 blue and 2 red areas.

Blue area = 2 $\times$ area of APC - area of the sector corresponding to the angle ACB

Area of APC = $\frac{1}{2}$ AP.AC
Because $\tan$ ($\angle ACP$) = AP/AC, AP = AC. $tan \angle ACP$
Also$\angle ACP$ =$\angle ACB$/2
Hence area of APC = $\frac{1}{2}$ (AC. $tan (\angle ACB$/2)).AC =$\frac{1}{2}$ ($r^2$ $tan (\angle ACB$/2))

Area of the sector subtended by x degrees = $\pi$ $r^2$ $\times$ ($x/360$)
So the area of the sector subtended by angle ACB = $\pi$ $r^2$ $\times$ ($\angle ACB$ $/360$)

So the blue area = 2$\times$ $\frac{1}{2}$ ($r^2$ $tan (\angle ACB$/2)) -$\pi$ $r^2$ $\times$ ($\angle ACB$ $/360$)

Red area = area of rectangle P*B*D*Q* - area of semi-circle = AP.(2r) -$\pi$ $r^2$/2 =
AC. $tan (\angle ACB$/2)$\times$(2r) - $\pi$ $r^2$/2 = $r^2$ $tan (\angle ACB$/2) -$\pi$ $r^2$/2

So the area of the holy leaf is:
8 $\times$ ($r^2$ $tan (\angle ACB$/2) - $\pi$ $r^2$ $\times$ ($\angle ACB$ $/360$)) + 2 $\times$ ($r^2$ $tan (\angle ACB$/2) - $\pi$ $r^2$/2)
= 12$r^2$ $tan (\angle ACB$/2) - $\pi$ $r^2$ ($\angle ACB/45$ + 1)

If$\angle ACB$ = 125 degrees, the area of the holy leaf is:
12 $\times$ $5^2$ $tan (125$/2) - $\pi$ $5^2$ ( 125/45 + 1) =279.59 $cm^2$

If$\angle ACB$ = 135 degrees, the area of the holy leaf is:
12 $\times$ $5^2$ $tan (135$/2) - $\pi$ $5^2$ ( 135/45 + 1) = 410.10 $cm^2$ > 279.59 $cm^2$

From our findings, some conclusions can be drawn as follows:
The boundary of the yellow area is greater than 2r$\pi$, which means the surface of the holy leaf has negative curvature.
As the angle ACB increases ($\angle ACB$ < 180 degrees), the curvature of the surface will increase; both parameters and areas of the holy leaf will also increase.