Dotty relationship
Can you draw perpendicular lines without using a protractor?
Investigate how this is possible.
Age
7 to 11
Challenge level
Problem
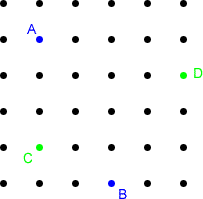
On the grid below, join the two blue dots, A and B, together with a
straight line.
Now join the green dots, C and D, with a straight line.
Now join the green dots, C and D, with a straight line.
Image
At what angle do the two lines cross?
Investigate the number of squares "along" and "down" from A to
B compared with the number of squares "along" and "up" from C to D.
What do you notice?
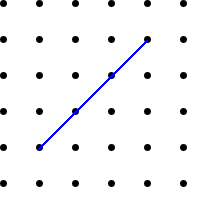
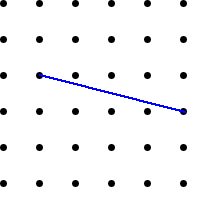
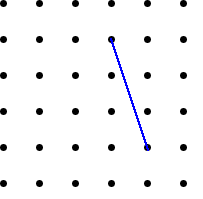
Using what you have found out, can you draw lines that are
perpendicular (at $90^{\circ}$) to the lines drawn below?
Image
Image
Image
Is there only one solution each time?
Do the two lines have to be the same length? Why or why
not?
Getting Started
You could use a protractor (angle measurer) to check the angle
between the two lines.
Is is possible to start from a different point when you are drawing the lines?
Is is possible to start from a different point when you are drawing the lines?
Student Solutions
Thank you to those of you who sent in solutions.
Several of you including Shuaib correctly identified that the lines AB and CD cross at $90$ degrees. Flora observes that the number of squares horizontally and vertically are swapped around when you draw a perpendicular line:
They are the same number of squares although the number of squares has been rotated.Flora goes on to observe that there is more than one solution each time :
because perpendicular lines can be any distance apart.
Alden and Jimmy from Woodstock Primary correctly point out that :
They do not have to be the same length because they can be any length as long as it's a $90$ degree angle.Teachers' Resources
Dotty Relationship
On the grid below, join the two blue dots, A and B, together with a straight line.Now join the green dots, C and D, with a straight line.
Image
At what angle do the two lines cross?
Investigate the number of squares "along" and "down" from A to B compared with the number of squares "along" and "up" from C to D. What do you notice?
Using what you have found out, can you draw lines that are perpendicular (at $90^{\circ}$) to the lines drawn below?
Image
Image
Image
Is there only one solution each time?
Do the two lines have to be the same length? Why or why not?