Screen shot
A moveable screen slides along a mirrored corridor towards a
centrally placed light source. A ray of light from that source is
directed towards a wall of the corridor, which it strikes at 45
degrees before being reflected across to the opposite wall and so
on until it hits the screen.
Problem
A moveable screen slides along a mirrored corridor towards a
centrally placed light source. A ray of light from that source is
directed towards a wall of the corridor, which it strikes at
$45^\circ $ before being reflected across to the opposite wall and
so on until it hits the screen.
If the screen is $20$ metres down the corridor from the light source and if the corridor is $2$ metres wide, find the position on the screen where the point of light appears.
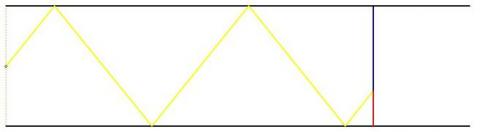
Part Two: Now remember that the screen is moveable. The distance, $d$, of the screen down the corridor can change, so the position where the point of light appears on the screen will depend on $d$. Can you find a function, expressing the position of the light on the screen in terms of $d$?
Part Three: If the ray leaves the source making an angle $\theta$ with the direction of the corridor, and the distance, $d$, of the screen down the corridor can still change, the position where the point of light appears on the screen will depend on $d$ and on $\theta$ . Can you find this function?
If the screen is $20$ metres down the corridor from the light source and if the corridor is $2$ metres wide, find the position on the screen where the point of light appears.
Image
Part Two: Now remember that the screen is moveable. The distance, $d$, of the screen down the corridor can change, so the position where the point of light appears on the screen will depend on $d$. Can you find a function, expressing the position of the light on the screen in terms of $d$?
Part Three: If the ray leaves the source making an angle $\theta$ with the direction of the corridor, and the distance, $d$, of the screen down the corridor can still change, the position where the point of light appears on the screen will depend on $d$ and on $\theta$ . Can you find this function?
Getting Started
At what distance down the corridor will the ray of light pass
through the centre line again?
At what distance down the corridor will the ray of light pass through the centre line again going in the same direction as it was initially?
At what distance down the corridor will the ray of light pass through the centre line again going in the same direction as it was initially?
Teachers' Resources
This problem gives opportunities to address processes that need
splitting into parts.
The path of the light ray switches direction at intervals, and handling that is crucial to the problem.
The path of the light ray switches direction at intervals, and handling that is crucial to the problem.
