Multiplication Square
Pick a square within a multiplication square and add the numbers on each diagonal. What do you notice?
Problem
Multiplicaton Square printable sheet - problem
Multiplication Square printable sheet - grid
Take a look at the multiplication square below:
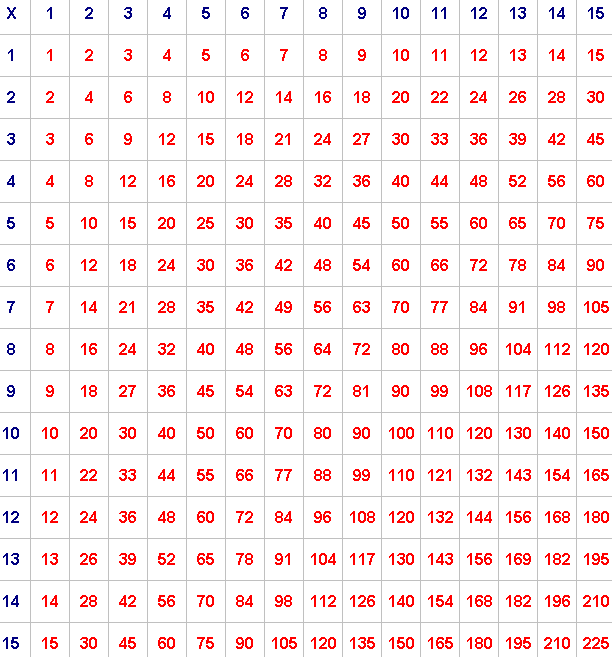
Pick any 2 by 2 square and add the numbers on each diagonal.
For example, if you take:
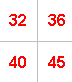
the numbers along one diagonal add up to $77$ ($32 + 45$)
and the numbers along the other diagonal add up to $76$ ($36 + 40$).
Try a few more examples.
What do you notice?
Can you show (prove) that this will always be true?
Now pick any 3 by 3 square and add the numbers on each diagonal.
For example, if you take:
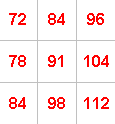
the numbers along one diagonal add up to $275$ ($72 + 91 + 112$)
and the numbers along the other diagonal add up to $271$ ($84 + 91 + 96$).
Try a few more examples.
What do you notice this time?
Can you show (prove) that this will always be true?
Now pick any 4 by 4 square and add the numbers on each diagonal.
For example, if you take:
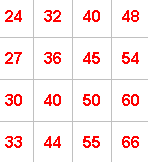
the numbers along one diagonal add up to $176$ ($24 + 36 + 50 + 66$)
and the numbers along the other diagonal add up to $166$ ($33 + 40 + 45 + 48$).
Try a few more examples.
What do you notice now?
Can you show (prove) that this will always be true?
Can you predict what will happen if you pick a 5 by 5 square, a 6 by 6 square ... an n by n square, and add the numbers on each diagonal?
Can you prove your prediction?
Click here for a poster of this problem.
Getting Started
For a general $2$ by $2$ square, the column headings could be $x$ and $(x + 1)$, and the row headings could be $y$ and $(y + 1)$.
For a general $3$ by $3$ square, the column headings could be $x$, $(x + 1)$ and $(x + 2)$, and the row headings could be $y$, $(y + 1)$ and $(y + 2)$.
If you are struggling with the algebra take a look at Partitioning revisited.
Student Solutions
Well done to Maulik aged 11 who sent in some nice work on this problem. Neil's solution is given below.
For a 2 by 2 square with column headings of x and x+1, and row headings of y and y+1, Neil says that:
For the two by two square you can always express it algebraically like this:
So the diagonal from top right to bottom left is:
$(x+1)y+x(y+1) = xy+y+xy+x = 2xy+x+y$
Lets call that Z.
The diagonal from top left to bottom right is:
$xy+(x+1)(y+1) = xy+xy+x+y+1 = 2xy+x+y+1$
So the first diagonal is Z and the second Z+1 so the diagonal from top left to bottom right is always 1 more than the diagonal from top right to bottom left.
For a 3 by 3 square with column headings of x, x+1 and x+2, and row headings of y, y+1 and y+2, Neil says that:
The 3 by 3 square looks like this:
The diagonal from top right to bottom left is:
$\begin{split}x(y+2)+(x+1)(y+1)+(x+2)y &= xy+2x+xy+x+y+1+xy+2y \\&= 3xy+3x+3y+1\end{split}$
The diagonal from top left to bottom right is:
$ \begin{split}xy+(x+1)(y+1)+(x+2)(y+2) &= xy+xy+x+y+1+xy+2x+2y+4 \\&= 3xy+3x+3y+5 \end{split}$
Let's say that $3xy+3x+3y = W$
The diagonal from top right to bottom left is W+1.
The diagonal from top left to bottom right is W+5. So the difference between the diagonals is 4.
More generally
Continuing with the same method:
Note that
1 = 1 ²
4 = 2 ²
10 = 1 ² + 3 ²
20 = 2 ² + 4 ²
35 =1 ² + 3 ² + 5 ²
56 = 2 ² + 4 ² + 6 ²
84 = 1 ² + 3 ² + 5 ² + 7 ²
Neil goes on to point out that the differences are the tetrahedral numbers.
Tetrahedral numbers are the sum of consecutive triangular numbers.
The formula is 1/6n(n+1)(n+2).
The first few tetrahedral numbers are 1, 4, 10, 20, 35, 56, 84, 120, ...
The tetrahedral numbers are found in the fourth diagonal of Pascal's triangle:
Teachers' Resources
This problem offers an opportunity:
- to notice and explain patterns in a multiplication square
- to use some algebraic techniques, in particular multiplying out brackets.
