Kissing
Problem
Two perpendicular lines are tangential to two identical circles that touch. What is the largest circle that can be placed in between the two lines and the two circles and how would you construct it?
Getting Started
The diagram is
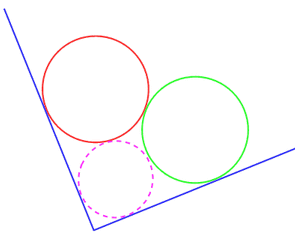
Without loss of generality you can takethe radii of the two identical circles to be 1 unit.
Using Pythagoras theorem can you then find the radius of the small circle? Don't worry if you get surds in the answer.
Student Solutions
Congratulations Tom Davie, Mike Gray and Ella Ryan of Madras College for your excellent team work on this problem. This is their solution; Tom wrote up the first part, Mike solved the equation and showed that there are two possible circles, and Ella described the construction of the smallest circle. Work like this is a real pleasure to read.
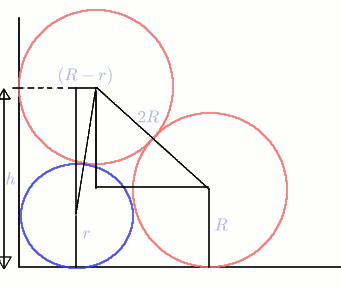
Let the radius of the small circle be $r$ and the radius of the larger circles be $R$. From the two triangles in the diagram formulae for $h$ can be found: $$h = r + \sqrt{(R + r)^2 - (R - r)^2} = r + 2\sqrt{rR}$$ and $$h = R + R\sqrt 2.$$ Hence
$$r_1 = R(3 + \sqrt 2 - 2\sqrt{2 + \sqrt2)})$$ $$r_2 = R(3 + \sqrt 2 + 2\sqrt{2 + \sqrt2)}).$$ Constructing the small circle. The small circle has radius $r$ (given in terms of $R$). $$r = R(3 + \sqrt 2 - 2\sqrt{2 + \sqrt2)})$$ To construct it you will need a pencil, compasses and straight edge.
- Set your compasses to the size of the radius of the larger
circles (length $R$) ).Image

-
Find $\sqrt 2 R$:
- take 2 lengths of $R$
- construct the perpendicular bisector of this line
- mark a length $R$ on the bisector
- the resulting diagonal has length $\sqrt 2 R$
Image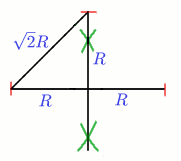
- Find $3R$ :
- draw 3 lengths of $R$
Image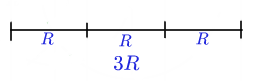
- Find$(\sqrt{2 + \sqrt 2})R$
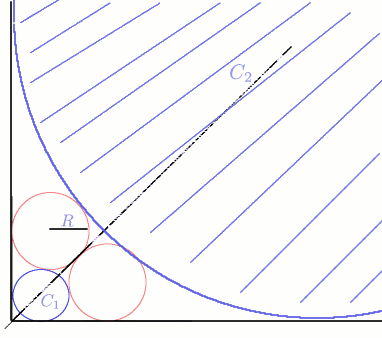
Ella's method uses the intersecting chord theorem: $x^2 = PA\times PB$Image
- draw line $AB$ of length$R +2R + \sqrt 2 R$
- mark the point$P$ such that$PA = R$
- draw the circle on $AB$ as diameter
- draw the chord perpendicular to $AB$ through $P$
- if this chord has length $2x$ then, by the intersecting chord
theorem, $$x^2 = R \times (2R + \sqrt2 R)$$ hence $$x = \sqrt{(2 +
\sqrt2)R}.$$
- Find $2(\sqrt {2 + \sqrt2})R$
- draw two lengths of $x$
-
- Find $r$
- subtract$2(\sqrt {2 + \sqrt 2})R$ from$\sqrt 2 R + 3R$
Image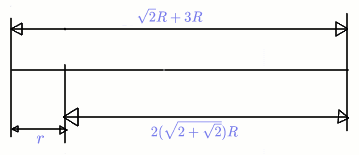
- Find the centre, $S$ of the small circleImage
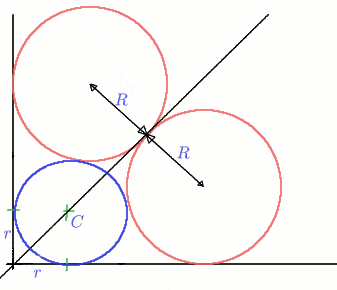
- set the compass to length to$r$
- mark off the length$r$ from the origin on both axes, giving the points where the circle touches the axes
- draw two arcs of radius $r$from these points, then the point where the arcs intersect is the centre$S$ of the small circle
- finally draw the circle centre $S$ radius $r$
APPENDIX 1 - DRAWING PERPENDICULAR LINES AND FINDING THE MIDPOINT OF A LINE
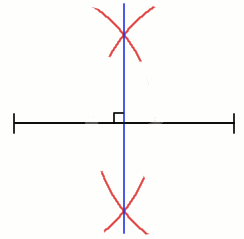
- set your compass to any length, retaining it throughout
- draw arcs above and below the line from each end of the line
- where the arcs intersect are two points on the perpendicular line
- where the perpendicular line and the original line cross is the midpoint.
