Degree Ceremony
Can you find the sum of the squared sine values?
Problem
Getting Started
WLOG (without loss of generality) let the length of the hypotenuse be equal to 1.
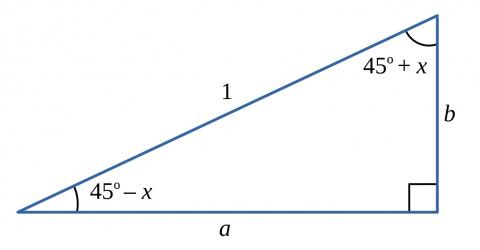
Can you find two different expressions for $a$? Can you find two different expressions for $b$?
Can you find a relationship connecting $\sin^2(45^{\circ} +x)$ and $\sin^2(45^{\circ}-x)$?
You can draw the graph of the sine function. What about the graph of $y = \sin^2 x$? What about the periodicity of this graph?
Student Solutions
Dylan from Brooke Weston and Soumya from King's Maths School in the UK used diagrams and two sines to solve the problem. Here is Dylan's work:
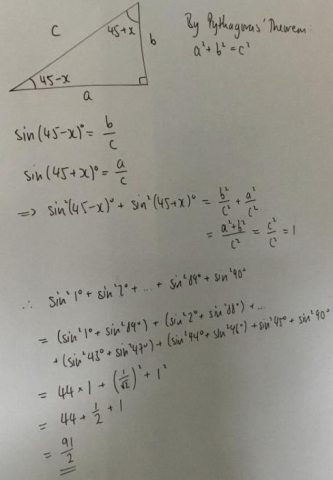
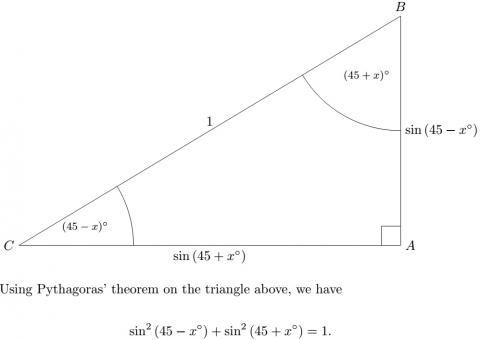
Soumya used a slightly different diagram, but the rest of the working was the same. Here is Soumya's diagram and the first line of Soumya's working:
Joshua, Gautham and Nishad used sines and cosines with another identity. This is Nishad's work:

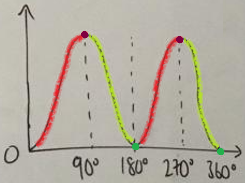
For the sum up to $\sin^2360^\circ$, Dylan and Joshua used graphs and symmetry. This is Joshua's work:
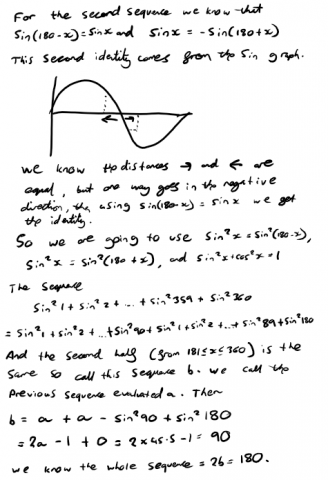
Dylan used a more graphical method which includes graph transformations. This is Dylan's work:
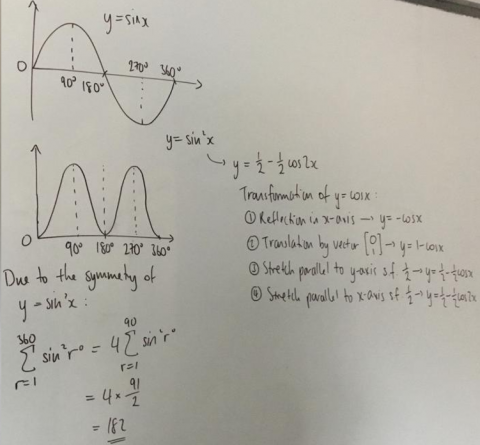
Note that Dylan's answer is slightly wrong. Can you use this diagram to see why?
Gautham and Soumya showed more terms in their working, so Dylan's lost terms are clearer. Here is Gautham's work (click on the image to see a larger version):

Soumya used sigma notation to express the same thing (click on the image to see a larger version):

Teachers' Resources
This problem gives students the chance to explore the relationships between the sine of different angles, and the symmetries of these.
As an alternative approach, students can use the graphs of trig functions to justify $\sin(90^{\circ} -x) = \cos x$ and use this to help find the value of the sum.
