It's a stormy day on the sea off the coast of Greece. The date
is around 520 BC. Fighting for his life, a man is heaved over the
side of a boat and dropped into the open water to die. His name is
Hippasus of Metapontum. His crime? Telling the world a mathematical
secret. The secret of the dangerous ratio.
The murder of Hippasus is a matter of legend, but the secret was
real, and certainly dangerous enough to the beliefs of those who
knew about it.
It was a secret owned by the school of Pythagoras. These early
Greek mathematicians (Pythagoras himself was born around 569 BC )
were obsessed with the significance of whole numbers and their
ratios. The Pythagorean's motto, carved above the entrance of the
school, was "All is number".
The inner circle of the school, the mathematikoi, believed that
the universe was built around the whole numbers. Each number from
one to ten was given a very special significance. Odd numbers were
thought to be male and even numbers female. Yet there was one
number that the Pythagoreans found terrifying, the number that
might have cost Hippasus his life for revealing its existence to
the world.
The name Pythagoras these days is best remembered for a
geometrical theorem, the one that tells us how to calculate the
lengths of the sides of a right angled triangle, and it is from
this theorem that the dangerous ratio emerges.
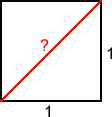
Imagine a simple square shape, each side 1 unit in length. How
long is the square's diagonal?
This seemingly harmless question was the trigger for the
Pythagoreans' disturbing discovery. The length of the square's
diagonal is easy to work out. It forms the long side of a triangle
with a right angle opposite, and two other sides of length 1 unit.
Thanks to Pythagoras' theorem we (and the Greeks) know that we can
work out the square of the length of the longest side of a
right-angled triangle by adding together the squares of the other
two sides. So we know the diagonal's length squared is $(1 \times
1) + (1 \times 1) = 2$, making the length of the diagonal itself $
\surd2 $. The number which when multiplied by itself makes 2. But
what is that number?
The square root of 2 isn't 1 because 1x1 is 1.
And it isn't 2, because 2x2 is 4.
It's something in between.
This wasn't a problem for the Pythagoreans. It was obviously a
ratio of two whole numbers. They only had to figure out what that
ratio was. At least that was the theory.
But after more and more frantic attempts, a horrible discovery
was made. There is NO ratio that will produce $ \surd 2 $ - it
simply can't be done. It's what we now call an irrational number,
not because it is illogical, but because it can't be represented as
a ratio of whole numbers.
This was what sent the Pythagoreans into such a spin that they
may have sacrificed poor Hippasus. If you believe that everything
is constructed from whole numbers, it is a terrible a shock to
discover that there is an everyday number, a 'real world' number
like the diagonal of a square, that doesn't fit your picture of the
world. It's a nightmare - and one from which the Pythagoreans would
never really recover.
How is it possible to prove that there is no ratio making $
\surd 2 $?
The logic is a little fiddly, but not too heavy.
Let's imagine that it is possible to come up with such a ratio
to produce $ \surd 2 $.
Let's call it $ \frac {top}{bottom}$.
Make this the simplest ratio you can have - cancelling out any
common factors.
Now, let's multiply both sides of the equation by itself,
so
$ \frac {top^2}{bottom^2} = 2 $
Next multiply both sides by $ bottom^2 $, ending up with
$ top^2 = 2 \times bottom^2 $
This means that $ top^2 $ must be an even number - because 2
times anything is even.
And that makes top an even number too - because an odd number
multiplied by itself is always odd.
What's more, if $ top^2 $ is an even number, so is $ bottom^2
$.
This is because an even number squared divided by 2 is still
even - and $ bottom^2 $ is $ top^2 $ divided by $2$.
That makes bottom an even number. So, top and bottom are both
even.
That means that each of them can be divided by 2.
But hang on. We started out by saying top and bottom were
chosen as the simplest possible ratio - any common factors had
already been divided out.
Now we are saying they have to have a common factor of 2. This
isn't possible. The only thing we can have wrong is our original
assumption, which was that $ \surd 2 $ is a rational number. You
simply can't have a ratio that makes up $ \surd 2 $. As Hippasus
discovered to his cost, that inscription over the Pythagorean
school All is number would
have to be extended to cope with more complex ideas than ratios of
whole numbers.
[Editor's note: If you have enjoyed this article you might
like to try
this interactivity . It is based on a slightly different proof
that the square root of 2 is irrational. This alternative proof can
be generalised to prove that all square roots of whole numbers that
are not square numbers are irrational, that is the square roots of
3, 5, 6, 7, 8, 10, 11 ...etc.]