Fence It
If you have only 40 metres of fencing available, what is the maximum area of land you can fence off?
Problem
Imagine you had $40$ one-metre sections of fencing.

What is the largest rectangular area of land you could fence off?
Now imagine you could build your fence up against a wall, so you only need to use the fence for three sides of the enclosure:

What is the largest area you can fence off now?
Now imagine you can attach the fence to the wall shown below, at the point marked X.

What is the largest area you can fence off now?
Extension
Could you enclose even greater areas if you had $40$m of flexible wire fencing that could fence off curves as well as straight lines?
Getting Started
Choose a length for your rectangle.
What must the width be if the fence is $40$m long?
What's the area?
What happens to the area when you change your chosen length?
Student Solutions
There are many ways to solve this one, and we received a lot of great anwsers. Since the questions appear to get harder and harder, let's start with the first problem.
What is the largest rectangular area of land you could fence off with 40m of fencing?
Amy tried lots of different possible side lengths for the rectangle. She used the base times height formula to get the area.
| base (m) | height (m) | area (m2) |
| 10 | 10 | 100 |
| 9 | 11 | 99 |
| 5 | 15 | 75 |
| 1 | 19 | 19 |
From this I think that the answer is 100m2 because the table shows the less
gap between the two numbers the larger the area and there isn't a gap
between 10 and 10 so it must be them.
This reasoning sounds right, well done. Don't worry that with a base and height of 10m the area fenced off makes a square; a square is just a special kind of rectangle! If we do a bit more thinking can we be absolutely certain there isn't some way of improving on 100m2? Nathan used the letters x and y to represent the base and the height of the rectangle.
If the sides are length x and y metres, then the perimeter of the rectangle is 2x+2y metres. Since this is all the fence we can use we must have 2x+2y=40. The area of the rectangle is x times y which I can write as xy.
From the first equation we know that 2y=40-2x so that y=20-x.
Then the formula for the area can be written
xy = x(20-x) = 20x-x2.
The largest value the expression 20x-x2 can take is 100, which is when x=10.
This is exactly right. If you draw a graph of the function 20x-x2 you'll see that it is highest at x=10, with a value of 200. There are also advanced techniques which can help find the highest point if you can't draw a graph.
A really special symmetry argument goes like this: in the equations 2x+2y=40 and Area=xy, there is nothing different between x and y; you could swap their names and the equations would be the same. This often means that the values of x and y should be the same.
What is the largest rectangular area you can fence off with a wall for one side?

Braiden noticed the following, and made a list of possible solutions.
The second question gives you the same amount of fence sections but only three sides of a rectangle need to be filled.
With trial and improvement he found that a 10 by 20 rectangle was the best. Well done. Can you see how the algebraic method with x and y might be used for this question too? We can say that the side opposite the wall is length x, and the other two fenced sides are length y.
The formula for the amount of fence used in the perimeter is x+2y=40.
The area is xy like before.
Notice x = 40-2y so we get:
Area = xy = (40-2y)y = 40y-2y2.
Now draw a graph or use advanced techniques to find the highest point of this function: 40y-y2. At y=10 we get an area of 200m2. Notice that in this case x=20, so the fenced area isn't a square.
What is the largest area you can fence off with the attachment point marked?
This third problem is the hardest, but both trial and improvement and algebra can help us find the answer. Kaedan noticed that you can split the area into smaller rectangles. The picture below might help too.

With the sides labelled what is the area covered? And what is the length of fence used? A few people managed to work this one out, well done!
First the area. We have 8x10=80m2 in the lower left corner.
The remaining rectangle has base x metres long, and height y-10.
Then the total area is 80+x(y-10).
This can be written Area = 80+xy-10x.
Now the perimeter. We use y+x+y-10 metres of fence. That is x+2y-10=40.
Some people made a table of values to work out the last bit, and the algebra works too.
The perimeter equation mean that x=50-2y, so the area equation is
Area = 80+50y-2y2-500+20y = 70y-2y2-420.
By plotting a graph or using another method we can see that the largest value is found at y=17.5. This makes an area of 192.5m2.
Extension: what about curved fences?
There are so many different shapes with curved sides, and you might not know a formula for the area for each one. Try a few shapes that you do know the area of and see what you can come up with. Can you beat the best values we found with rectangles and straight sides? Do you need different shapes or will one always win?
Teachers' Resources
Why do this problem?
This problem challenges students to work systematically while applying their knowledge of areas of rectangles. It offers opportunities for higher level mathematical thinking (optimising and graphing) in a context that doesn't require sophisticated mathematical content.
This problem could be revisited when students are older and are able to use algebraic techniques (forming quadratic expressions, maximising by completing the square).
Possible approach
This printable worksheet may be useful: Fence It.
"Imagine you had $40$ one-metre sections of fencing, and you wanted to make a rectangular enclosure. On your whiteboards, sketch a possible rectangle you could make that uses all $40$m. Write the area of your rectangle inside."
Tabulate students' responses on the board. Select the largest area that has been found so far: "Is this the largest possible area we can make with $40$m of fencing?" Once the $10$m square with area $100$m$^2$ has been found, "How can we be convinced that a larger area isn't possible?" Give students a few minutes to think about the question in pairs and develop some convincing arguments. Circulate and listen in on conversations to identify which pairs have something worth sharing. Look out for diagram representations similar to this one:
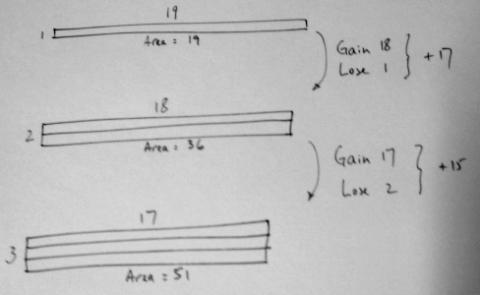
or tables of values like this one:

Bring the class back together and invite any pairs whose interesting insights you noticed to share their thoughts. Use this to write an agreed 'convincing argument' why a square gives the maximum area, modelling the level of rigour that you expect them to come up with in their own justifications later on.
Now set the second problem: "Imagine you had a long wall that you could use as one of the sides of your enclosure, so your $40$ metres of fencing only has to go round three sides of the rectangle. Use the ideas we have shared to work with your partner and find the biggest possible enclosure now. Make sure you have a justification to convince everyone that your area is the biggest possible."
This worksheet has all three parts of the problem on, so you could hand this out to students who finish the second task quickly.
Before the end of the lesson, allow some time for students to present their findings, focussing particularly on their justifications.
Key questions
What would the width of the rectangle be if the length is 1m? 2m? 3m? ...
How can I be sure I have found the maximum possible area?
Possible support
Share the diagrams above to help students to represent their trial-and-improvement strategies in a clear way that shows how the area changes.
Possible extension
Some students may use algebra to represent the scenarios and use graphical methods to find/justify the optimal solution.
Relaxing the straight lines constraint would allow students to consider some circle geometry:
"Could you enclose even greater areas if you had 40m of flexible wire fencing that could fence off curves as well as straight lines?"
