Fred the Class Robot
Billy's class had a robot called Fred who could draw with chalk
held underneath him. What shapes did the pupils make Fred draw?
Age
7 to 11
Challenge level
Problem
Billy's school has a paved area at the front:
Image
Billy's class had a robot called Fred who could draw with chalk held underneath him.
Image
Billy's teacher drew lines and numbers on the paved area in front of the school so that they could tell Fred where to go.
Image
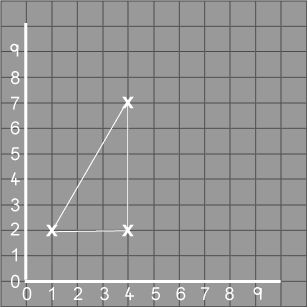
Billy's teacher put a little cross on the point $(1, 2)$ and the children put Fred on the cross. Fred moved to $(4, 7)$, then to $(4, 2)$ and then back to $(1, 2 )$. Fred's chalk drew a line to show where he had been.
Image
"What shape has Fred drawn?" asked Billy's teacher.
"A triangle!" shouted all the class.
All the children wanted to make Fred draw shapes.
Tom had the first turn. He got Fred to go from $(6, 1)$ to
$(6, 6)$, and then to $(1, 6)$ and $(1, 1)$ and back to $(6,
1)$.
What shape had Fred drawn?
Vicky made Fred go from $(2, 1)$ to $(7, 2)$, and then to $(9,
4)$ and $(4, 6)$ and then $(1, 5)$ and back to $(2, 1)$.
What shape had Vicky made Fred draw?
Billy thought very hard when it was his turn. He made Fred go
from $(7, 4)$ to $(4, 7)$, and then to $(1, 4)$ and $(4, 1)$ and
back to $(7, 4)$.
What shape had Billy made Fred draw?
If Billy had made Fred start at the same place, $(7, 4)$, how
else could a shape like this be drawn on the $9$ by $9$ axes? (It
doesn't have to be the same size as Billy's first shape.)
Getting Started
Perhaps it would help to draw out what Fred is doing on squared paper?
Have you counted the number of sides of each shape and looked at the angles? You might like to move your paper around to help you see what each shape is.
Have you counted the number of sides of each shape and looked at the angles? You might like to move your paper around to help you see what each shape is.
Student Solutions
Thank you to Amber from CCHS and two groups of children from Moorfield Junior School (Helen, Katie, Amy and Pauline were one group and the second consisted of Luke, Vicky and Alex) who correctly answered the first parts of the problem. Luke, Vicky and Alex said:
The first shape that Tom drew was a square.The shape that Vicky drew was an irregular pentagon.
Billy also made Fred draw a square.
Amber went on to explain:
We know it is a square and not just any diamond/rhombus because it has four right angles whereas any other kind of diamond/rhombus would have two acute angles and two obtuse angles.Pupils from Mrs Simmons Class at Aqueduct Primary School sent in a wonderful solution to the final part of the question. They say:
We cut squares out, firstly small squares, $1$ square wide, then $2$ squares wide and so on. Then we put the corner of a square onto ($7,4$) and marked the points out. We did this for every size until we could not find any more coordinates that would fit.We found a pattern forming and so we coloured in the squares in lots of different colours and layered them onto the grid.
We then listed all the coordinates we had found on a separate piece of paper. We have named each square a letter, to correspond with the list of coordinates.
They sent the following images to show their solutions:
Image
They also sent the coordinates which Fred would have to go to in order to draw all the squares:
A $( 7 , 4 ) ( 7, 3 ) ( 6 , 3 ) ( 6 , 4 ) ( 7 , 4 )$B $( 7 , 4 ) ( 6, 4 ) ( 6 , 5 ) ( 7 , 5 ) ( 7 , 4 )$
C $( 7 , 4 ) ( 7, 5 ) ( 8 , 5 ) ( 8 , 4 ) ( 7 , 4 )$
D $( 7 , 4 ) ( 8 , 4 ) ( 8 , 3 ) ( 7 , 3 ) ( 7 , 4 )$
E $( 7 , 4 ) ( 7, 6 ) ( 9, 6 ) ( 9 ,4 ) ( 7 , 4 )$
F $( 7 , 4 ) ( 6, 4 ) ( 6 , 5 ) ( 7 , 5 ) ( 7 , 4 )$
G $( 7 , 4 ) ( 9, 4 ) ( 9 , 2 ) ( 7 , 2 ) ( 7 , 4 )$
H $( 7 , 4 ) ( 7, 2 ) ( 5 , 2 ) ( 5 , 4 ) ( 7 , 4 )$
I $( 7 , 4 ) ( 4, 4 ) ( 4 , 7 ) ( 7 , 7 ) ( 7 , 4 )$
J $( 7 , 4 ) ( 7, 1 ) ( 4 , 1 ) ( 4 , 4 ) ( 7 , 4 )$
K $( 7 , 4 ) ( 3, 4 ) ( 3 , 8 ) ( 7 , 8 ) ( 7 , 4 )$
L $( 7 , 4 ) ( 7, 0 ) ( 3 , 0 ) ( 3 , 4 ) ( 7 , 4 )$
M $( 7 , 4 ) ( 2, 4 ) ( 2 , 9 ) ( 7 , 9 ) ( 7 , 4 )$
But this isn't all of the squares. Mrs Simmons class also found these:
Image
And here are the coordinates:
A $( 7 , 4 ) ( 6, 5 ) ( 7 , 6 ) ( 8 , 5 ) ( 7 , 4 )$B $( 7 , 4 ) ( 8, 5 ) ( 9 , 4 ) ( 8 , 3 ) ( 7 , 4 )$
C $( 7 , 4 ) ( 8 , 3 ) ( 7 , 2 ) ( 6 , 3 ) ( 7 , 4 )$
D $( 7 , 4 ) ( 6, 3 ) ( 5 , 4 ) ( 6 , 5 ) ( 7 , 4 )$
E $( 7 , 4 ) ( 5, 6 ) ( 7 , 8 ) ( 9 , 6 ) ( 7 , 4 )$
F $( 7 , 4 ) ( 5, 2 ) ( 3 , 4 ) ( 5 , 6 ) ( 7 , 4 )$
G $( 7 , 4 ) ( 9, 2 ) ( 7 , 0 ) ( 5 , 2 ) ( 7 , 4 )$
H $( 7 , 4 ) ( 4, 1 ) ( 1 , 4 ) ( 4 , 7 ) ( 7 , 4 )$
Well done! You have obviously gone about this in a very logical way.
Teachers' Resources
Fred the Class Robot
Billy's school has a paved area at the front:
Image
Billy's class had a robot called Fred who could draw with chalk held underneath him.
Image
Billy's teacher drew lines and numbers on the paved area in front of the school so that they could tell Fred where to go.
Image
Billy's teacher put a little cross on the point $(1, 2)$ and the children put Fred on the cross. Fred moved to $(4, 7)$, then to $(4, 2)$ and then back to $(1, 2 )$. Fred's chalk drew a line to show where he had been.
Image
"What shape has Fred drawn?" asked Billy's teacher.
"A triangle!" shouted all the class.
All the children wanted to make Fred draw shapes.
Tom had the first turn. He got Fred to go from $(6, 1)$ to $(6, 6)$, and then to $(1, 6)$ and $(1, 1)$ and back to $(6, 1)$.
What shape had Fred drawn?
Vicky made Fred go from $(2, 1)$ to $(7, 2)$, and then to $(9, 4)$ and $(4, 6)$ and then $(1, 5)$ and back to $(2, 1)$.
What shape had Vicky made Fred draw?
Billy thought very hard when it was his turn. He made Fred go from $(7, 4)$ to $(4, 7)$, and then to $(1, 4)$ and $(4, 1)$ and back to $(7, 4)$.
What shape had Billy made Fred draw?
If Billy had made Fred start at the same place, $(7, 4)$, how else could a shape like this be drawn on the $9$ by $9$ axes? (It doesn't have to be the same size as Billy's first shape.)
Why do this problem?
This problem is one in which learners will be practising the use of coordinates and in addition will be developing their understanding of properties of shapes. The problem may challenge their preconceptions of how a shape "should be" oriented!
A similar activity could be set up practically in the classroom or outside using a floor turtle. In any case squared paper should be provided.
Key questions
Would it help to draw out what Fred is doing on squared paper?
Have you counted the number of sides of each shape and looked at the angles?
What makes the shape a square and not another four-sided shape?