Fixing It
A and B are two fixed points on a circle and RS is a variable diamater. What is the locus of the intersection P of AR and BS?
Problem
$A$ and $B$ are two fixed points on a circle and $RS$ is a variable diamater.
What is the locus of the intersection $P$ of $AR$ and $BS$?
Getting Started
Think about angle $APB$.
You might like to use dynamic geometry software to help with this problem. You can download geogebra for free from geogebra.org. We have pre-drawn a diagram if this is useful to you.
Student Solutions
Image
|
Image
|
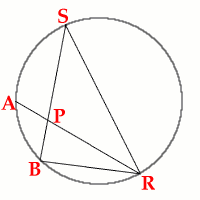
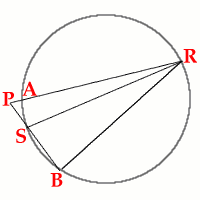
$\mathbf{A}$ and $\mathbf{B}$ are fixed points on a circle,
while $\mathbf{RS}$ is a variable diameter. $\mathbf{P}$ is the
intersection of $\mathbf{AR}$ and $\mathbf{BS}$. We make the
conjecture that the locus of $\mathbf{P}$ isa a second circle
through the points $\mathbf{A}$ and $\mathbf{B}$.
Edward Wallace of Graveney
School, Tooting sent a very good proof of this
conjecture.
First consider the two cases illustrated in the given
diagrams. It is impossible to have $\mathbf{R}$ and $\mathbf{S}$
both on the minor arc of the circle. The other two cases, where
$\mathbf{R}$ and $\mathbf{S}$ exchange positions, and $\mathbf{P}$
is outside the original circle, are proved similarly.
Case 1
Both $\mathbf{R}$ and $\mathbf{S}$ are on the major arc
$\mathbf{AB}$ so that $\mathbf{P}$ is inside the original
circle.
Case 2
$\mathbf{S}$ is on the minor arc $\mathbf{AB}$ and
$\mathbf{R}$ on the major arc so that $\mathbf{P}$ is outside the
original circle.
In Case 1, $\angle\mathbf{ARB}$ is unchanging (invariant) as
$\mathbf{R}$ moves on the circumference because angles subtended on
the circumference of a circle by a fixed arc of the circle are
equal. Hence ($\angle \mathbf{ARB} = m^o$ (constant). Also $\angle
\mathbf{RBS}=90^o$ because the angle subtended by a diameter is a
right angle.
It follows that $\angle \mathbf{RPB}=(90 - m)^o$ because the
angles of the triangle $\mathbf{BRP}$ add up to $180^o$.
Hence $\angle \mathbf{APB}$ is constant and equal to $(90 +
m)^o$ because angles on a line add up to $180^o$. This is a
necessary and sufficient condition for P to lie on the
circumference of a circle of which $\mathbf{AB}$ is a chord. Let us
call this arc $\mathbf{AP_{1}B}$ to emphasise the fact that, in
this case, $\mathbf{P_1}$ is inside the original
circle.
In Case 2, exactly the same argument applies, giving $\angle
\mathbf{ARB} = m^o$ (the same value as in Case 1) and
$\angle\mathbf{RBS}=90^o$, but in this case $\angle\mathbf{APB}$ is
the same angle as $\mathbf{RPB}$ so $\angle\mathbf{APB}=(90 - m)^o$
(again constant).
As before, this is a necessary and sufficient condition for
$\mathbf{P}$ to lie on the circumference of a circle of which
$\mathbf{AB}$ is a chord. We call this arc $\mathbf{AP_{2}B}$ to
emphasise the fact that now $\mathbf{P_2}$ is outside the original
circle.
Note that:
$\angle\mathbf{AP_{1}B} + \angle\mathbf{AP_{2}B} = (90 + m)^o
+ (90 - m)^o = 180^o$ and hence $\mathbf{AP_{1}BP_{2}}$ is a cyclic
quadrilateral which confirms that the locus of $\mathbf{P}$ is a
single circle (and not two arcs of different circles).
