Coordinates and Descartes
The person who is credited with our coordinates system is a man called Descartes. If you look here then you can find out how he was inspired by a fly!
Coordinates are one way of describing the position of something. If you are trying to find your way to a place you've never been to before, chances are, you'll use a map. Has it ever occurred to you how that map was made? Or perhaps who first thought of the idea of designing maps? We're here to answer these questions for you.
What is a map?
A map is a way of showing position, described by a coordinate system, using lines, areas and points. The process of making maps is called cartography . Maps are drawn for many different purposes:
- To find a point on the earth's surface
- To show patterns e.g. an earthquake hazard map
- As a navigational tool e.g. on the World Wide Web
The person designing a map (the cartographer ) may use colour, size, shape, numerical value, texture, pattern and orientation to help get across information.
Here we will concentrate on maps which help us to locate a position on the earth's surface.
The History of Map Making
We cannot be completely sure of where the first map was made. It seems that maps were being developed at similar times in different parts of the world. Some of the earliest maps were drawn on clay tablets by the Babylonians, possibly around 2000BC. This one was found at the town of Ga-Sur, approximately 200 miles north of the site of Babylon:

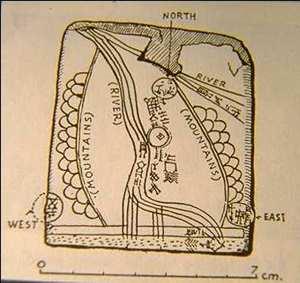
Left: Clay tablet from Ga-Sur
Right: Interpretation of tablet
Used with permission www.henry-davis.com/MAPS/
However, another map was found during excavations at the site of a town called Catal Hy"uk in Turkey. It is thought that this map shows Catal Hy"uk itself and maybe dates back to even earlier -- around 6000 BC:

Map of Catal Hy"uk, Turkey
Used with permission http://www.henry-davis.com/MAPS/
In 500BC, Greek scholars were the first to suggest that the world was spherical. They based this on the altitude of stars and how ships appear on the horizon. Aristotle saw that the earth casts a round shadow on the moon. This had great impact on map drawing and led Eratosthenes to calculate a surprisingly accurate figure for the circumference of the earth. He went on to produce a world map:

Used with permission http://www.henry-davis.com/MAPS/
Have you ever looked closely at a globe or a world atlas? In a similar way to the x and y coordinates that we are familiar with, a special coordinate system is used. Eratosthenes was the first person to try to draw a map of the world based on a system of lines of latitude and longitude .
Lines of latitude are imaginary horizontal lines that circle the globe. We can think of this as circles of different sizes:
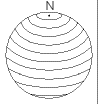
The longest is at the equator.
The shortest are at the north and south poles where they shrink to a point.
Lines of latitude are also called parallels as they run parallel to the equator.
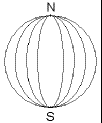
Lines of longitude are imaginary lines reaching from pole to pole. We can think of them as looking like segments of an orange.
Lines of longitude are also known as meridians .
Hipparchus built on the work of Eratosthenes and was the first to give the positions of places on the earth as coordinates using latitude and longitude. In fact, these coordinates are angles:
The latitude of the equator is 0 degrees.
The latitude of the north pole is +90 degrees.
The latitude of the south pole is -90 degrees.
All lines of longitude cross the equator and as this is circular, it can be divided into 360 degrees. The longitude of a point can be taken as where its meridian line crosses the equator. However, this depends on which line of longitude is taken as 0 degrees.
There were many twists in the tale to follow. Ptolemy, another Greek, wrote a book in eight volumes called "Geography" which contained maps of the known world at that time. All these were based on a curved globe. Ptolemy showed how to represent a sphere on a flat piece of paper:
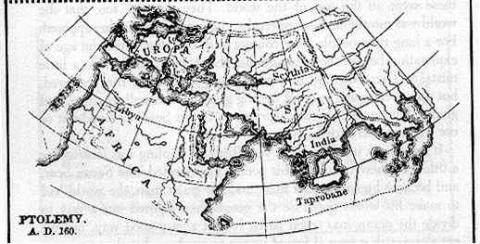
Used with permission www.henry-davis.com/MAPS
Map-making did not really develop further until after the 12th century AD. During the Age of Exploration (15th century) sailors were discovering new lands and it was a complicated task to draw up the maps. However, this meant that the position of new places on earth had to be worked out.
In 1514, Werner, a German, translated Ptolemy's Geography and suggested a way of measuring longitude using the moon. Unfortunately, he was not able to be accurate enough at that time. Many European explorers tried to tackle the problem of calculating longitude. Gemma Frisius, from the Netherlands, used a clock to keep time as he travelled in an east-west direction. He then compared this time with the local time at his destination to work out the total distance. This in fact proved to be a very good method but unfortunately the clocks at that time were not accurate enough.
Producing world maps became a great challenge and countries started offering rewards to encourage people to solve the problem. It was believed that maths and astronomy were the key to finding longitude. Observatories were set up in both Paris and London.
Each country had different approaches. The French used the idea of the movement of Jupiter's moons which had initially been proposed by Galileo in 1616. The English however concentrated on the position of our moon. Both groups continued to work on developing an accurate clock.
Between the two, methods were eventually found and at last longitude could be measured accurately.
In 1884, an International Meridian Conference was held. The meridian which passed through the Royal Observatory in Greenwich, London was given 0 degrees longitude. Greenwich was chosen as it was already used as zero on over 70% of navigation maps at that time, so this decision would benefit the most people. The line at 0 degrees longitude is known now as the Prime Meridian or Greenwich Meridian .
Places to the east of this line are measured from +0 degrees to +180 degrees
Places to the west of this line are measured from -0 degrees to -180 degrees This means that the lines at +180 degrees and -180 degrees are in fact the same.
And Now?
With improved technology, map making has become much easier. Computers, space science, aerial photography and electronic distance-measuring instruments have all helped to make cartography more accessible. There is much more to a map than meets the eye, wouldn't you agree? It just goes to show how useful maths is! These websites will give you more information:
