Co-operative problem solving: pieces of the puzzle approach
The content of this article is largely drawn from an Australian publication by Peter Gould that has been a source of many successful mathematics lessons for both children and student-teachers. (See publication details at end of article). It presents a style of problem-solving activity that has the potential to benefit ALL children in a class, both mathematically and socially, and is readily adaptable to most topics in mathematics curricula.
What is the Pieces of a Puzzle Approach?
Essentially, the 'Pieces of the Puzzle Approach' is a deductive reasoning activity in which each group member is given a piece of information to share with the rest of the group. The mathematical solution cannot be found without everyone's contribution. Thus, an important aspect of the approach is that the group assumes 'ownership' of the task yet individuals retain personal responsibility within the group. This style of activity was developed and used effectively by the EQUALS group in the U.S.A (1989).
To support the approach, a set of essential work rules must be established (based on the work of Burns 1992).
Rules
- You are responsible for your own work and behaviour
- You must be willing to help any group member who asks
- You may only ask the teacher for help if everyone in the group has the same question
These rules assist in avoiding some of the pitfalls of co-operative group work. Once the children have had experience with these rules, the situation of one person dominating by collecting all the pieces of information and taking control should not occur. Similarly, a group member should not opt out of the activity and sit back and let the rest of the group solve the problem. The ability of the children to successfully follow the rules will improve with each session, and will be influenced by teacher led discussions about the purpose of each rule.
The structure of this approach is intended to provide positive opportunities for:
- Risk taking - pupils are more likely ask questions of each other and put forward ideas in a small group situation, particularly with Rule 2 in place.
- Mathematical language development - usually the clues for the tasks are communicated with words. The group needs to negotiate their interpretation of the mathematical vocabulary. They also must talk to each other, listen to others and explain their ideas clearly.
- Peer coaching - pupils are able to clarify their understanding of mathematical concepts, correct misconceptions and test out ideas during the process of finding a collective solution to the problem.
- Teacher's role as a facilitator and observer - the independence of the groups gives the teacher freedom to move around the class, observe language and strategies, interact with groups as required and assess their progress.
- Effective learning - the tasks generally incorporate the manipulation of physical objects to produce a final product, which promotes the linking of verbal knowledge with visual imagery.
- Mixed ability class teaching - the features listed above combine to make this approach particularly suited to use with mixed ability classes. Every child should be able to make a contribution to the problem solving process, learn from the activity and have received attention from the teacher when needed.
Forming the Groups
There are, of course, many ways to organise children into groups. Unless the teacher has specific reasons for doing otherwise, a random mix method is best for this type of co-operative problem solving.
Random Mix by the Cards
Here is one way to achieve a random mix of pupils using a pack of ordinary playing cards. To form seven groups of four children, use all four card suits from one (Ace) to seven. Shuffle this pack and have each child choose a card. All the sevens form a group, all the sixes form a group and so on.

- Diamonds - team manager - responsible for assisting teacher to get group's attention at specified signal and reminding the group of the 'rules';
- Spades - equipment manager - responsible for collecting and returning materials, and ensuring all group members have access to the materials;
- Hearts - recorder - noting significant information, steps in solution, or preparation of finished product (such as the model, drawing or chart);
- Clubs - spokesperson - responsible for reporting the group's efforts and/or solutions
Lesson Structure
Introduction: This type of problem solving activity is well suited to developing and clarifying mathematical ideas that have already been introduced in other lessons. Therefore, in introducing the task to the class, the teacher can make links to previous work. If the mathematical vocabulary contained in the problem is of particular concern, then key terms should be revised.
Group work: The groups are formed and each child in a group is given one clue card. To maintain 'ownership' of the piece of information, the child may not physically give away the clue-card, but must be responsible for communicating the content to the group. Each pupil's role is now to work within his/her group to solve the puzzle, following the set of work rules. The teacher must also take care to follow these rules, and not take back responsibility for the task by interfering with the problem-solving processes or offering help before being asked by the whole group.
As always, it is advisable to have an extension question ready for a group that finishes before the others. It is also useful to have one or two 'extra' clues ready. These can be used to allow the inclusion of an extra group member, to give help to a group that is 'stuck', or to assist 'checking' when a group thinks it has finished the task.
Plenary - It is important for groups to report on their problem-solving processes as well as confirming the correctness of their end product. The teacher can use questions focus on particular issues and highlight points that have been observed during the session. For example:
Examples of Problems
An important advantage of the Pieces of the Puzzle Approach is that teachers can make up their own problems to suit whatever topic is appropriate. This is done by working back-wards from the final product (such as a model) or answer (such as a number), and then designing a set of essential clues, plus a couple of extra clues. Make use of any maths resources in the school such as multi-link cubes, pattern blocks, Polydron shapes or other construction materials. A visual focus should be provided, even for number problems, so make use of digit cards, number lines, Hundred Charts etc.
It is wise to test the clues out on someone else if possible. It takes a bit of time, but the same problems can be recycled in years to come. Asking children to invent their own problems once they gain some experience is an excellent extension exercise, as well as an interesting assessment opportunity.
The following problems are only examples of the sort of tasks that can be done, and should be used as models to generate many more problems. Clue cards A, B, C, D are usually the essential pieces of information, E and F are extra clues.
Number Hunts
Each group requires a 'Hundred Chart' (10 x 10 grid showing the numbers 1 to 100 or 0 to 99). The aim is to deduce the mystery number.
|
A
PETER'S NUMBER
Peter's number is even.
|
B
PETER'S NUMBER
When you add the digits,
you get an odd number.
|
|
C
PETER'S NUMBER
Peter's number is a multiple of six.
|
D
PETER'S NUMBER
Peter's number is a multiple of four.
|
|
E
PETER'S NUMBER
One of the digits is NOT double the other digit.
|
F
PETER'S NUMBER
Peter's number is in the bottom half of the chart.
|
(More than one answer is possible until Clues E & F are incorporated)
Stick Figures
Each group needs a handful of sticks, all of the same length - such as matches, ice-cream or lolly sticks, or drinking straws. The aim is to arrange some of the sticks to make either a single shape or shapes-combinations (depending on the level of complexity).
|
A
STICK FIGURE 3
There are three squares in the figure.
|
B
STICK FIGURE 3
The big square has an area four times larger than
each of the small squares.
|
|
C
STICK FIGURE 3
Eleven sticks are used to make afigure.
|
D
STICK FIGURE 3
One small square shares a side with the other
small square.
|
|
E
STICK FIGURE 3
The bottom half of the figure is a rectangle.
|
F
STICK FIGURE 3
Three sticks lie inside the large square.
|
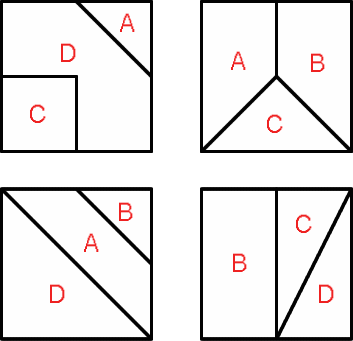
Fractured Shapes
The clues in this type of problem are non-verbal. In the example below, the squares are cut up by the teacher and each member of a group-of-four is given three pieces marked with the same letter. The aim is for the group to make four complete squares.
Operations
Each group needs a set of digit cards (two or three copies of the digits 0-9) and a template of the algorithm, in this example a two-column sum
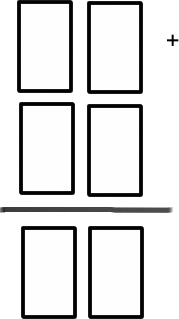
|
A
FIND THE SUM 1
All of the digits are even numbers.
|
B
FIND THE SUM 1
Adding the digits in the top number gives 10.
|
|
C
FIND THE SUM 1
The 'ones' digit in the first number is the same as the
'tens' digit in the answer.
|
D
FIND THE SUM 1
Both the digits in the second number gives 4.
|
|
E
FIND THE SUM 1
The difference between the digits in the answer is 2.
|
F
FIND THE SUM 1
Adding the digits in the second number gives 4.
|
Cube Models
Each group must have some cubes for these construction problems.
|
A
MODEL VIEWS 2
8 cubes are used to build the model. |
B
MODEL VIEWS 2
The view from the top
looks like this.
Image
|
|
C
MODEL VIEWS 2
The view from the front
looks like this.
Image
|
D
MODEL VIEWS 2
The view from the right side
looks like this.
Image
|
|
E
MODEL VIEWS 2
The view from one corner looks like this.
Image
|
F
MODEL VIEWS 2
The view from one corner looks like this.
Image

|
References
Burns, M. (1992) About Teaching Mathematics, Maths Solution Publications: California Erickson, T. (1989) Get It Together, EQUALS: University of California.
Gould, P. (1993) Co-operative Problem Solving in Mathematics, Mathematical Association of N.S.W. Australia. ISBN 0-7310-1371-9 (Available through the Australian Association of Mathematics Teachers Catalogue code MAN466 - http://www.aamt.edu.au/ )
