History of fractions
Did you know that fractions as we use them today didn't exist in Europe until the 17th century? In fact, at first, fractions weren't even thought of as numbers in their own right at all, just a way of comparing whole numbers with each other. Who first used fractions? Were they always written in the same way? How did fractions reach us here? These are the sorts of questions which we are going to
answer for you. Read on ...
The word fraction actually comes from the Latin "fractio" which means 'a breaking down, a division'. To understand how fractions have developed into the form we recognise, we'll have to step back even further in time to discover what the first number systems were like.
From as early as 1800 BC, the Egyptians were writing fractions. Their number system was a base 10 idea (a little bit like ours now) so they had separate symbols for 1, 10, 100, 1 000, 10 000, 100 000 and 1 000 000. The ancient Egyptian writing system was all in pictures which were called hieroglyphs and in the same way, they had pictures for the numbers:
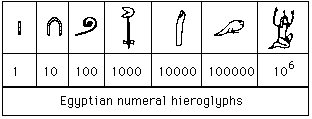
Here is an example of how the numbers were made up:

Could you write down 3 581 in hieroglyphics?
The Egyptians wrote all their fractions using what we call unit fractions. A unit fraction has 1 as its numerator (top number). They put a mouth picture (which meant part) above a number to make it into a unit fraction.
For example:
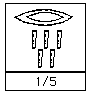
They expressed other fractions as the sum of unit fractions, but they weren't allowed to repeat a unit fraction in this addition. For example this is fine:
$${3\over4} = {1\over2} + {1\over4}$$
But this is not:
$${2\over7} = {1\over7} + {1\over7}$$
The huge disadvantage of the Egyptian system for representing fractions is that it is very difficult to do any calculations. To try to overcome this, the Egyptians made lots of tables so they could look up answers to problems.
In Ancient Rome, fractions were only written using words to describe part of the whole. They were based on the unit of weight which was called the as. One "as" was made up of 12 uncia so fractions were centred on twelfths. For example:
${1\over12}$ was called uncia
${6\over12}$ was called semis
${1\over24}$ was called semuncia
${1\over288}$ was called scripulum (one twenty-fourth of an uncia)
As with the Egyptian system, the words made it very difficult to do calculations.
The Babylonians were the first people to come up with a more sensible way of representing fractions. In fact they did this before the Romans' methods but there was no contact between the two civilisations. The Babylonians lived in the country we now call Iraq in the Middle East. Their number system was organised around the number 60, so we say it is base 60. In other words they grouped numbers
into 60s, whereas we group into 10s. (We still use base 60 in our measurement of time and angles.) However, they also grouped into 10s and so only had two symbols, one for a unit and one for a 10:
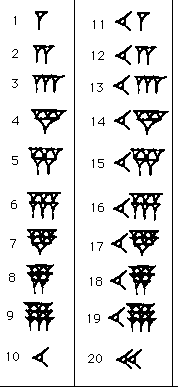
Here are the numbers from 1 to 20.
Can you see the symbol for 1?
What about the symbol for 10?
How would you write 47?
The Babylonians simply extended their numbers to include fractions in sixtieths, as we do for tenths, hundredths etc. However, they didn't have a zero or anything like a decimal point. This made reading numbers very confusing as they could be interpreted in different ways. Here's an example:
From the table above, you can see that the two numbers are 12 and 15. Now, this is where it becomes confusing. This could mean several different things:
| x60 | Units | Sixtieths | Number |
| $12$ | $15$ | $12 + {15\over60} = 12 {15\over60}$ | |
| $12$ | $15$ | $720 + 15$ |
So, although the Babylonians had a very sophisticated way of writing fractions, it did have its drawbacks. Around 311BC they began using zero as a placeholder so this made things easier, but without a decimal point, it was still difficult to distinguish fractions from whole numbers. We are now reaching the end of our journey through the history of fractions! The format we know today comes
directly from the work of the Indian civilisation. The success of their way of writing fractions is due to the number system they created which has three main ideas:
i) Each figure has a symbol which isn't like the value it represents
ii) The value of the figure depends on the position of it within the entire number
iii) A zero is needed to mean nothing and also to fill the place of units that are missing
By about 500AD, the Indians had developed a system from a way of writing called brahmi, which had nine symbols and a zero. Again, this was devised a long time before some of the other ways of counting we have already discussed. However it was only through the trading of the Arabs that these Indian numerals were spread to Arabia where they were used in the same form. The chart below shows how
these brahmi symbols became the numbers we know today:
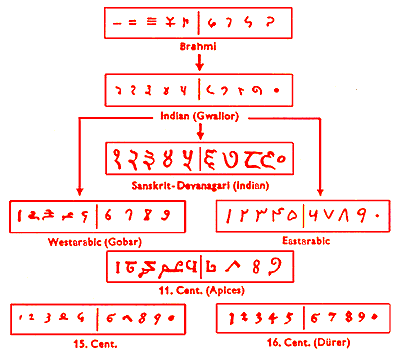
In India fractions were written very much like we do now, with one number (the numerator) above another (the denominator), but without a line. For example:
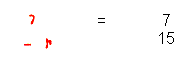
So here we have the fraction as we now recognise it. It is amazing to think how much thought has gone into the way we write it down, isn't it? Perhaps next time you use fractions, you'll remember this.
All images reproduced by kind permission from https://mathshistory.st-andrews.ac.uk/ .
If you'd like to know more, check out these websites:
- https://mathshistory.st-andrews.ac.uk/
- http://www.math.buffalo.edu/mad/Ancient-Africa/
- http://www.gosai.com
"The Universal History of Numbers" by Georges Ifrah, published by Harvill, is also a fantastic source of information.
Perhaps you could find out about other civilisation's number systems.For information on the Greeks try:
http://www.math.tamu.edu/~dallen/history/gr_count/gr_count.html
