Some(?) of the Parts
Problem
A circle touches the lines $OA$ extended, $OB$ extended and $AB$ where $OA$ and $OB$ are perpendicular.
Show that the diameter of the circle is equal to the perimeter of the triangle.

Student Solutions
Jeremy from Nottingham High School was the first to crack this one with the neatest proof that the diameter of the circle is equal to the perimeter of the triangle $OAB$ and Peter from Konstanz sent a similar proof. Other good proofs came in from Hannah and Sarah of St Philomena's School, Carshalton, Steven Cunnane of Norwich School, and James of The Robert Smyth School, Market Harborough.
If you take $OA$ as 1 unit then the perimeter $OAB$ and the diameter of the circle are equal to $2 + \sqrt{2}$ units.
Let the circle touch $OA$, $OB$ and $AB$ at $X$, $Y$ and $Z$ respectively.
Let $C$ be the centre of the circle and $R$ the radius. It is easy to prove that $OYCX$ is a square.
Then $AZ = AX$, since the tangents from a point to a circle are equal. Similarly, $BZ = BY$.
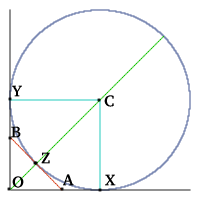
$OA + OB + AB$
$= OA + OB + AZ + BZ$
$= OA + OB + AX + BY$
$= OX + OY$
$= 2R$.
