Age
5 to 11
| Article by
Jenni Way
 | Published

The development of spatial and geometric thinking: the importance of instruction



This article follows two previous articles: "The early years" and "Co-ordinating space in drawings".

When considering resources for shape and space many teachers ask themselves questions such as:

 

  • What are the benefits of using shape puzzles, tangrams and other mosaic-type resources?
  • The children like playing with them, but do they learn anything?
  • How could activities be structured to really teach some geometric ideas?

This article provides some answers to these questions by looking at levels of geometric thinking and the types of activities required to develop this thinking.

 

The van Hiele Levels of Geometric Thought

There is some well-established research that has been influencing school curriculum development internationally for many years now, but the practical details are still unknown to most teachers. This research began in the 1950's with a husband and wife team in the Netherlands, Pierre and Dina van Hiele. Pierre van Hiele has continued to develop the theory over the years, and many other researchers around the world have investigated its basis and application in various ways. The main theory emphasises that despite some natural development of spatial thinking, deliberate instruction is needed to move children through several levels of geometric understanding and reasoning skill. It is based on the firm belief that it is inappropriate to teach children Euclidean geometry following the same logical construction of axioms, definitions, theorems and proofs that Euclid used to construct the system. Children don't think on a formal deductive level, and therefore can only memorise geometric facts and 'rules', but not understand the relationships between the ideas, if taught using this approach.

The van Hiele theory puts forward a hierarchy of levels of thinking spanning the ages of about five years through to academic adults. Originally there were five levels, that have been adapted and renamed by various researchers, but now van Hiele concentrates on the three levels that cover the normal period of schooling. The main content focus is on two-dimensional (plane) shape.

Level 1: Visual

This level begins with 'nonverbal thinking'. Shapes are judged by their appearance and generally viewed as 'a whole', rather than by distinguishing parts. Although children begin using basic shape names, they usually offer no explanation or associate the shapes with familiar objects. For example, a child might say, "It's a square because it looks like one", or "I know it's a rectangle because it looks like a box". This could be likened to young children's ability to recognise some words by sight, before they understand the individual letter sounds and how they blend together to form words.

Level 2: Descriptive

At this level, children can identify and describe the component parts and properties of shapes. For example, an equilateral triangle can be distinguished from other triangles because of its three equal sides, equal angles and symmetries. Children need to develop appropriate language to go with the new specific concepts. However, at this stage the properties are not 'logically ordered', which means that the children do not perceive the essential relationships between the properties. So, with the equilateral triangle for example, they do not understand that if a triangle has three equal sides it must have three equal angles.

Level 3: Informal Deduction

In this level, the properties of shapes are logically ordered. Students are able to see that one property precedes or follows from another, and can therefore deduce one property from another. They are able to apply what they already know to explain the relationships between shapes, and to formulate definitions. For example, they could explain why all squares are rectangles. Although informal deduction such as this forms the basis of formal deduction, the role of axioms, definitions, theorems and their converses, is not understood.

 

Activity Phases to Develop Geometric Thinking

Included in van Hiele's theory is a sequence of five phases of activity types that are designed to promote the movement of children's thinking from one level to the next. There are a variety of ways to use these phases when planning lessons. For example, a teacher might choose to deal with the topic of squares, and so design all the tasks to involve the manipulation, construction, discussion and so on, of squares. Another way to use the phases is to take a more general approach and explore a number of different shapes simultaneously. Cycling through these phases using materials such as tangrams and various mosaic puzzles enables children to build a rich background in visual and descriptive thinking about shapes and their properties.
 
Activity Examples: Traditional seven-piece tangram sets are commonly available and so have been used as the basis of activities to illustrate each phase. The topic is not 'Tangrams', but the 'Properties of 2D Shapes'. The activities are not really age specific, but are probably best suited to children in the range of 7 to 10 years old. It is desirable for each child to have his or her own tangram, so multiple copies could be made from card and stored in envelopes. The pieces in the example below have been numbered for easy reference in this article, but it is also useful to do this (or colour-code) with the children's sets. (Find or make a tangram set and use it to try out the activities as you read. Instructions for folding a tangram can be found here or one can easily be drawn using grid paper as shown below).
 



 

The development of spatial and geometric thinking: The Importance of Instruction.



Phase 1: Inquiry

Learning begins with play! The children should be encouraged to freely explore the materials and hence discover some properties and structures. While the children are playing, the teacher has the opportunity to observe and informally assess the children's thinking and language.

Example: Give each child a tangram set and simply ask 'What can you do with these pieces?' Encourage the children to share and talk about the shapes and pictures they have made. Allow plenty of time for children to freely explore the pieces. During this play the children will become familiar with the size and shape of the pieces, and they begin to see how they fit together. In other words, they begin to discover the properties and relationships.

Phase 2: Direct Orientation

Activities are presented in such a way that children's attention is focussed on particular characteristics of the shapes or puzzle pieces. Ideas for directed activities will come from watching the children at play, as well some pre-planned tasks.

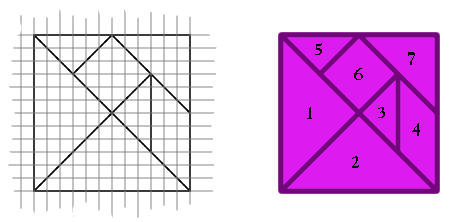
Example: In free play a child may have used pieces 3 and 5 to make piece 6. So ask the children to find out whether all the pieces can be made from two smaller pieces. They might do this by fitting the two pieces together on top of the larger piece. Other questions to explore are:

 

  • Which pieces can be made from three other pieces? Have the children record what they find by tracing around the shapes.
  • One activity will often lead to another; How many different ways can the largest triangle (1) be made using the other pieces?
  • Choose two shapes. How many different shapes can you make with them? Draw them all and give them names. Use three shapes to make a new shape (not like one of the other pieces). Trace around it. How many ways can you make this shape? Can you make it with and without the numbers showing? Draw all the solutions.
From these activities the children gain a more specific understanding of the properties of the shapes. They will notice the lengths of sides, some that are equal and others that are half or double the length of others. They will visualise how the angles will fit together and how to flip and turn the shapes to fit various spaces.
 
Phase 3: Explication
 
This involves tasks and games that deliberately develop the vocabulary associated with the ideas that have been encountered so far, while continuing to explore the properties of the shapes. The teacher clarifies terms the children are already using and introduces new terms. Activities that encourage the children to use the vocabulary as they talk and write about their experiences should be utilised.
 
Example: During some workshops, the teacher names the shapes; square, isosceles triangle, and parallelogram, as well as other vocabulary associated with the properties; similar, equal sides, equal angles, right angle, symmetry and parallel sides. Questions like the following will provide opportunities for the terms to used as well as clarifying the associated concepts:
 
  • Which shapes have a right angle? Match them up in a pile. (What size are the other angles?)
  • Trace around each shape on paper and cut it out. How many lines of symmetry does each shape have?
  • What is the same about all the triangles?
  • Which shapes have parallel sides?
  • Which shapes have sides the same length within themselves? Which shapes have sides the same length as other shapes? half/double the length?
  • Play 'Mystery Bag' where a child feels a hidden shape and describes it to the rest of the class, who try to name the shape.
The children should be encouraged to explain and demonstrate what they find out, perhaps using pieces on an overhead projector, or making a display poster.
 
Phase 4: Free Orientation
 
The children engage in activities and problem-solving tasks that are open-ended or can be completed in different ways. The aim is for children to utilise what they have learned and become more proficient.
 
Example: The children should engage in more challenging tasks, that draw on the knowledge and skills previously developed; such as:
 
  • How many ways can you make a square from some or all of the pieces?
  • Complete classic tangram puzzles of outlines of birds and animals.
  • Draw a completed tangram square (like the one illustrated above) on an 8x8 square grid, examine the pieces carefully in relation to the grid, then work out a way to enlarge all the pieces.
Phase 5: Integration
 
Opportunities are given for the children to pull together their new knowledge and reflect on it as a whole. They should be able to express or summarise what they have learned in some way.
 
Example : Small groups of children can design charts, class books and displays that present what they have learned about the tangram shapes. Pairs of children could prepare "What shape am I?" cards which could be used by individuals or in team games. Class games like "Twenty Questions" will help children to logically organise their knowledge of properties of the shapes. Individual assessment might be carried out by giving children open-ended tasks, like 'Choose a shape and write everything you can about it', and 'Choose another shape and design a What shape am I? Card'.

 

Outcomes of the Five Phases of Activities

 
As a consequence of engaging in a series of activities such as those described above, the majority of children will have progressed from simply recognising some shapes, to being able to discuss the shapes in terms of specific geometric properties and perhaps make some comparisons between shapes. In other words, they will have moved from Level 1 Visual thinking to Level 2 Descriptive thinking in regards to the shapes treated in the activities. Although the knowledge and vocabulary developed in respect to this specific set of shapes will assist in the study of different shapes, many more similar experiences will be needed to develop geometric thinking about different shapes. For example, the puzzle shapes presented below would provide good opportunities for the children to explore types of triangles and quadrilaterals. (Note that it is easily copied using equilateral-triangle dot or grid paper).



 

The development of spatial and geometric thinking: The Importance of Instruction.
References
 
Fuys, Geddes & Tischler. (1988) The van Hiele model of Geometric Thinking Among Adolescents. Journal of Research in Mathematics Education Monograph 3.
 
Pegg, J. & Davey, G. (1991). Levels of Geometric Thought. The Australian Mathematics Teacher. Vol.7. No.2.
 
Van Hiele, P. (1999) Developing Geometric Thinking Through Activities that Begin with Play. Teaching Children Mathematics. February 1999. (pp. 310-316)