Multiplication series: illustrating number properties with arrays
An introduction on using arrays can be found here.
Whether taught formally in school or not, the properties that apply to numbers in operations are encountered by children during their learning of mathematics. A sound understanding of these properties provides a good basis for developing operations, including mental calculation. The operation of addition comes easily to most children, but working with multiplication requires more sophisticated
thinking and therefore usually needs more support. Modelling number properties involving multiplication using an array of objects not only allows children to represent their thinking with concrete materials, but it can also assist the children to form useful mental pictures to support memory and reasoning.
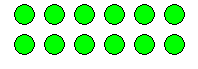
Commutative property
Division as the Inverse Operation of Multiplication
Of the four operations, division is the most troublesome for young students. Full understanding of division tends to lag well behind the other operations. For many children opportunities to explore the concept with concrete materials are curtailed well before they perceive the relationships between division and the other four operations. One such relationship, the inverse relationship between
division and multiplication, can be effectively illustrated using arrays.
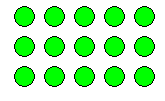
Further exploration of the array reveals two more ways of expressing inverse relationships: $5 \times3 = 15$ and $15 \div 3 = 5$ . The word problems can be adapted to describe these operations and highlight the similarities and differences between the four expressions modelled by the one array.
Distributive property of multiplication over addition
This rather long title not only names one of the basic properties that govern our number system, it also names a personally invented mental strategy that many people regularly use. This strategy often comes into play when we try to recall one of the handful of multiplication facts that, for various reasons, are difficult to remember. For example, does this kind of thinking seem familiar?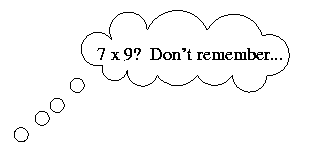
"I know $7 \times7$ is $49$.
I need two more lots of $7$, which is $14$.
So if I add $49$ and $14$... that makes $63$.
Ah yes! $7 \times9=63$.'"
Symbolically, this process can be represented as...
\begin{eqnarray} 7 \times 9 &=& 7 \times (7 + 2)\\ &=& (7 \times 7)+(7 \times 2) \\ &=& 49 + 14 \\ &=& 63 \end{eqnarray}
Another way to explain this process is through an array.
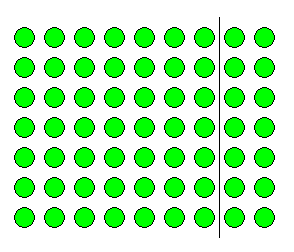
- The whole array represents $7 \times9$ ($7$ rows of $9$)
- The smaller array to the left of the line shows $7 \times7$ ($7$ rows of $7$).
- The small array to the right of the line shows $7 \times2$ ($7$ rows of $2$).
- It can now be easily seen that $7 \times9$ is the same as $(7 \times 7) + (7 \times2)$, which leads to $49 + 14 = 63$.
