Tubular stand
If the radius of the tubing used to make this stand is r cm, what is the volume of tubing used?
Problem
A square stand designed to protect surfaces from hot pans is made from four $10 \; \text{cm}$ long pieces of cylindrical wooden dowel joined at the corners with $45$ degree mitres.
If the radius of the dowel used to make a stand is $0.5 \; \text{cm}$, what is the volume of wood used?
Image

If I doubled the volume of wood used but did not change the radius of the dowel - what would the outside dimension of the stand be?
If, instead, I doubled the radius of the dowel but kept the same volume of wood, what would the outside dimension of the stand be then?
By looking in more detail at the effects of changing one of the variables at a time, can you describe any relationships between the volume of wood, the radius and the length of the dowel used?
Getting Started
The corners of the stand have to be considered and this means that each individual section is not a cylinder. However a little careful manipulation will reveal that the problem is far from insurmountable.
For the generalisation it might help to reduce the number of variables you work with to two at a time...
What is the relationship between the length and the volume if the radius is fixed?
Is there a way you can represent the relationship without just trying to describe it in words?
Student Solutions
There were a number of partial solutions but this well explained one is almost entirely the work ofAndrei of Tudor Vianu National College and shows how "obvious" the answer is with a little visualising and careful reasoning.
Image
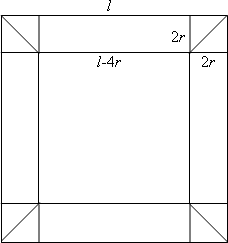
Let $l$ be the exterior length of the cylinders and $r$ - the radius of the cylinders.
In the first solution, I have $4$ cylinders (the $4$ squares length $l-4r$ and $2r$) and $8$ half-cylinders - cylinders cut through the diagonal (the 8 small right-angled triangles from the figure).
Each of the four cylinders has the volume: $ V_1 = \pi r^2 (l - 4r)$
Each of the half-cylinders has a volume of half a cylinder: $ V_2 = \frac{1}{2} \times \pi r^2 \times 2r = \pi r^3$ Now, the total volume of the tubular stand is: $ V = 4 \times V_1 + 8 \times V_2 = 4\pi r^2 (l - 2r) $
With the second method, I arrange the $8$ half-cylinders to make $4$ bigger cylinders, and these $4$ to the bigger ones. The height of one 'big' cylinder is $(l - 2r)$, and the total volume is: $$ V = 4 \pi r^2 (l - 2r) $$ which is exactly the result obtained above. Substituting the numerical values: $l = 10 \; \text{cm}$ and $r =0.5 \; \text{cm}$, I obtain:
$$ V = 4 \pi \times 0.25 \times(10 - 1) = 9 \pi = 28.27 \; {\text{cm}}^3 $$
If the volume wood would be double $(18 \pi)$, then the outside dimension of the dowel would be: \begin{eqnarray} 18 \pi &=& 4\pi \times 0.25 (l -1) \\ l - 1 & =& 18 \; \text{cm}\\ l &=& 19 \; \text{cm}\end{eqnarray} If the volume of wood would be the same but the radius would be $1 \; \text{cm}$, then the outside dimension would be: \begin{eqnarray} 9 \pi &=& 4\pi (l - 2) \\ l - 2 &=& \frac {9}{4} \\ l &=& 4.25 \; \text{cm}\end{eqnarray} The general formula for the volume of the dowel (proved above) is: $$ V = 4 \pi r^2 (l - 2r) $$ One could see that the volume is proportional to the square of the radius, and in the limit of long outside dimensions, proportional to the outside dimension.
Teachers' Resources
Two pieces of dowel placed end-to-end and rotated should reveal a "neat" fit. Some cardboard wrapping paper tubes or toilet paper holders can be very useful in illustrating this point.
