Salinon
This shape comprises four semi-circles. What is the relationship between the area of the shaded region and the area of the circle on AB as diameter?
Problem
The shape below is constructed using four semi-circles. It is called a Salinon.
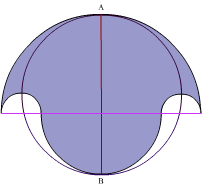
What is the relationship between the area of the shaded region and the area of the circle whose diameter is $AB$?
Getting Started
The diameters of the circles are related. This might prove useful.
Student Solutions
Correct solutions were received from Roy of Allerton High School, Hannah of St Helen's and St Katharines and Andre of Tudor Vianu National College, Bucharest. All used the method below. Well done to you all.
The areas are equal.
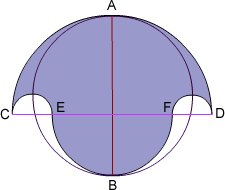
The salinon is composed of semicircles on $CD$, $EF$, $CE$ and $FD$.
Now we can find the area of the salinon in terms of these semicircles as follows;
Let the big semicircle on $CD$ have a radius of $a$, the medium one on $EF$ be radius $b$. Then the small circles on $CE$ and $FD$ have a radius of $\frac{a-b}{2}$ and the circle on $AB$ has radius $ \frac{a+b}{2}$.
The area of the semicircle on $CD$ is $ \pi \times \frac{a^2}{2}$.
The bottom semi circle (on $EF$) has an area of $ \pi \times \frac{b^2}{2}$.
The two smaller semi circles, on $CE$ and $FD$ together make a circle whose area is $ \pi \times \left(\frac{a-b}{2}\right)^2 $
The total area of the salinon is:
the top semi circle + the bottom semi circle - the two smaller identical semi circles or $$ \pi \frac{a^2}{2} + \pi \frac{b^2}{2} - \pi\left(\frac{a-b}{2}\right)^2 $$ multiplying out all the brackets you get $$ \frac{\pi}{4} \times (a^2 + b^2 + 2ab) $$
Now for the area of the main circle with diameter $AB$:
the radius of the circle is $$ \frac{a+b}{2}$$ so the area of it is $$ \pi\times \left(\frac{a+b}{2}\right)^2 $$ which, when multiplied out is the same as the area of the salinon.
Teachers' Resources
Why do this problem?
The solution uses the formula for the area of a circle and gives practice in geometrical reasoning and manipulating algebraic expressions.
Possible approach
This printable worksheet may be useful: Salinon.
Start with a class discussion about the radii of the 4 semi-circles and the circle on AB as diameter. When the students have understood that there are only two unknowns involved, and the other radii can all be expressed in terms of the two unknowns, then they are ready to write down the areas and answer the question which they could do individually.
Dynamic geometry software could be a useful tool to aid investigation but this is not essential.
Key questions
If the blue semicircles have radii a and b what can you say about the other radii?
Possible support
Try Round and Round
Possible extension
Partly Circles is a similar problem.
Learners could make up their own problems of this type.
